Question

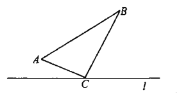
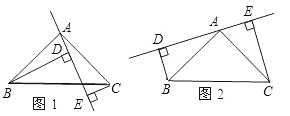
【题目】如图1，△ABC中，AB=AC，∠BAC=90°，直线l经过点A，过B、C两点分别作直线l的垂线段，垂足分别为D、E．

（1）如图1，△ABD与与△CAE全等吗？请说明理由；

（2）如图1，BD=DE+CE成立吗？为什么？

（3）若直线AE绕A点旋转到如图2位置时，其它条件不变，BD与DE、CE关系如何？请说明理由．

Answer 1

【答案】（1）△ABD≌△CAE；（2）成立；（3）DE=BD+CE．

【解析】

（1）根据已知条件易证得∠BAD=∠ACE，且根据全等三角形的判定可证明△ABD≌△CAE；

（2）根据全等三角形的性质及各线段的关系即可得结论．

（3）DE=BD+CE．根据全等三角形的判定可证明△ABD≌△CAE，根据各线段的关系即可得结论．

（1）△ABD≌△CAE，理由如下：

∵∠BAC=90°，∴∠BAD+∠CAE=90°．

∵CE⊥AE，∴∠ACE+∠CAE=90°，∴∠ACE=∠BAD；

又∵BD⊥AE，CE⊥AE，∴∠ADB=∠CEA=90°．

在△ABD和△CAE中，∵∠BAD=∠ACE，∠ADB=∠CEA，AB=CA，∴△ABD≌△CAE（AAS）；

（2）成立，理由如下：

∵△ABD≌△CAE，∴BD=AE，AD=CE；

∵AE=DE+AD，∴BD=DE+CE；

（3）DE=BD+CE．理由如下：

∵∠BAC=90°，∴∠BAD+∠CAE=90°．

∵CE⊥AE，∴∠ACE+∠CAE=90°，∴∠ACE=∠BAD；

又∵BD⊥AE，CE⊥AE，∴∠ADB=∠CEA=90°．

在△ABD和△CAE中，∵∠BAD=∠ACE，∠ADB=∠CEA，AB=CA，∴△ABD≌△CAE（AAS），∴BD=AE，AD=CE；

∵DE=AE+AD，∴DE=BD+CE．