题目内容
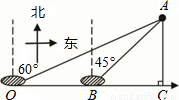
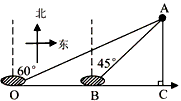
 如图,在A岛周围25海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°方向,轮船继续前行20海里到达B处发现A岛在北偏东45°方向,该船若不改变航向继续前进,有无触礁的危险?(参考数据:
如图,在A岛周围25海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°方向,轮船继续前行20海里到达B处发现A岛在北偏东45°方向,该船若不改变航向继续前进,有无触礁的危险?(参考数据:| 3 |
分析:要得出有无触礁的危险需求出轮船在航行过程中离点P的最近距离,然后与暗礁区的半径进行比较,若大于则无触礁的危险,若小于则有触礁的危险.
解答:解:根据题意,有∠AOC=30°,∠ABC=45°,∠ACB=90°,
所以BC=AC,
于是在Rt△AOC中,由tan30°=
,
得
=
,
解得AC=
≈27.32(海里),
因为27.32>25,
所以轮船不会触礁.
所以BC=AC,
于是在Rt△AOC中,由tan30°=
| AC |
| OC |
得
| ||
| 3 |
| AC |
| 20+AC |
解得AC=
| 20 | ||
|
因为27.32>25,
所以轮船不会触礁.
点评:此题主要考查解直角三角形的有关知识.通过数学建模把实际问题转化为解直角三角形问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
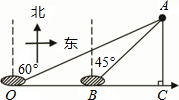
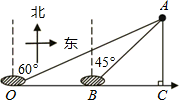 如图,在A岛周围25海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°方向,轮船继续前行20海里到达B处发现A岛在北偏东45°方向,该船若不改变航向继续前进,有无触礁的危险?(参考数据:
如图,在A岛周围25海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°方向,轮船继续前行20海里到达B处发现A岛在北偏东45°方向,该船若不改变航向继续前进,有无触礁的危险?(参考数据: ≈1.732)
≈1.732)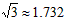 )
) 
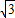 ≈1.732)
≈1.732)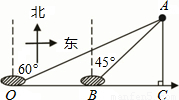
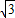 ≈1.732)
≈1.732)