题目内容
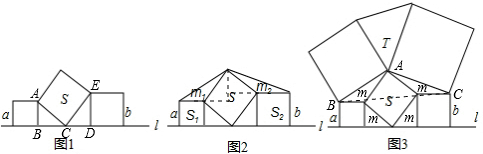
在直线l上摆放着三个正方形（1）如图1，已知水平放置的两个正方形的边长依次是a，b斜着放置的正方形的面积S=
a2+b2
a2+b2
，两个直角三角形的面积和为ab
ab
；（均用a，b表示）（2）如图2，小正方形面积S1=1，斜着放置的正方形的面积S=4，求图中两个钝角三角形的面积m1和m2，并给出图中四个三角形的面积关系；
（3）图3是由五个正方形所搭成的平面图，T与S分别表示所在的三角形与正方形的面积，试写出T与S的关系式，并利用（1）和（2）的结论说明理由．
分析：（1）根据题意，可以证得中间的两个三角形全等，再根据勾股定理，即可得出答案；
（2）求出两个钝角三角形的底边和高，然后根据三角形的面积公式求解即可；
（3）利用勾股定理分别求出S和T的值，然后比较求解即可．
（2）求出两个钝角三角形的底边和高，然后根据三角形的面积公式求解即可；
（3）利用勾股定理分别求出S和T的值，然后比较求解即可．
解答：解：（1）如图1所示：∵三个四边形均为正方形，
∴∠ACB+∠BAC=90°，∠ACB+∠DCE=90°，AC=CE，
∴∠BAC=∠DCE，
∵∠ABC=∠CDE=90°，
∴△ABC≌△CDE，
∴BC=DE=a，AB=CD=b，
∴S△ABC+S△CDE=ab，
同时AC2=AB2+BC2，
∵两个正方形的面积分别为a2，b2，
∴S=a2+b2，
（2）如图2所示，a=1，斜正方形边长c=2，b=
，
由30°角和60°角易求出面积为m1的三角形底边长为1，高为
，故m1=
；
面积为m2的三角形边长为
，高为1，故m2=
．
结论：四个三角形的面积相等．
（3）S=T．如图3所示，首先由（2）知：T=S△ABC，
设小正方形边长为a，大正方形边长为b，
由（1）知：S=a2+b2，又图中四个小三角形的面积m=
ab，
S△ABC=a2+b2+（a2+b2）+4×
ab-
（a+b）（2a+2b）=a2+b2=S，
∴S=T．
∴∠ACB+∠BAC=90°，∠ACB+∠DCE=90°，AC=CE，
∴∠BAC=∠DCE，
∵∠ABC=∠CDE=90°，
∴△ABC≌△CDE，
∴BC=DE=a，AB=CD=b，
∴S△ABC+S△CDE=ab，
同时AC2=AB2+BC2，
∵两个正方形的面积分别为a2，b2，
∴S=a2+b2，
（2）如图2所示，a=1，斜正方形边长c=2，b=
| 3 |
由30°角和60°角易求出面积为m1的三角形底边长为1，高为
| 3 |
| ||
| 2 |
面积为m2的三角形边长为
| 3 |
| ||
| 2 |
结论：四个三角形的面积相等．
（3）S=T．如图3所示，首先由（2）知：T=S△ABC，
设小正方形边长为a，大正方形边长为b，
由（1）知：S=a2+b2，又图中四个小三角形的面积m=
| 1 |
| 2 |
S△ABC=a2+b2+（a2+b2）+4×
| 1 |
| 2 |
| 1 |
| 2 |
∴S=T．
点评：本题考查了勾股定理的运用，结合正方形的面积求解公式求解．
练习册系列答案
相关题目
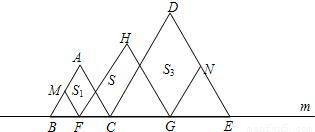
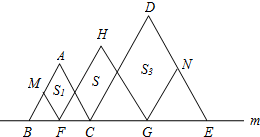如图，在直线m上摆放着三个正三角形：△ABC、△HFG、△DCE，已知BC=
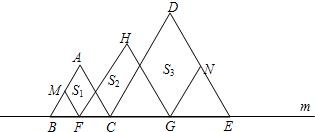如图，在直线m上摆放着三个正三角形：△ABC、△HFG、△DCE，已知BC=GE，F、G分别是BC、CE的中点，FM∥AC，GN∥DC．设图中三个平行四边形的面积依次是S1，S2，S3，若S1+S3=20，则S2等于（ ）
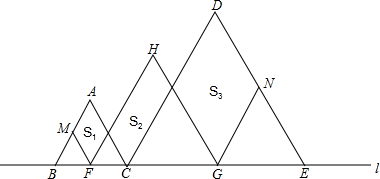若S1+S3=10，则S2=
CE，F、G分别是BC、CE的中点，FM∥AC，GN∥DC．设图中三个平行四边形的面积依次是S1，S，S3，若S1+S3=10，则S= ．