题目内容
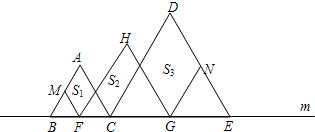 如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=GE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=20,则S2等于( )
如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=GE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=20,则S2等于( )| A、7 | B、8 | C、9 | D、10 |
分析:首先要弄清的是S1与S△OFC(即a)、S3与S△GNE(即b)的关系;以前者为例,若设△OFC中,OC边上的高为h,则a=
OC•h,而S1=OA•h;由于BF=FC,且△BMF、△FOC都是等边三角形,故OA=BF=FC=OC,由此发现S1=2a,同理S3=2b;由于△OFC和△GNE都是等边三角形,所以它们都相似,且相似比为1:2(因为BC=GE=2FC),故b=4a,a+b=5a=
(S1+S3)=10,由此可得a=2,b=4;然后按照上面的方法证S2与S△PCG(即b)的关系,从而得到S2的面积.
| 1 |
| 2 |
| 1 |
| 2 |
解答: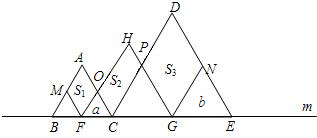 解:如图;(a、b分别表示△OFC、△GNE的面积)
解:如图;(a、b分别表示△OFC、△GNE的面积)
∵F、G分别是BC、CE的中点,
∴△BMF、△OFC以及△CPG、△GNE都是全等的等边三角形;
∴S△CPG=b;
设M到AC的距离为h,则S1=OA•h,a=
OC•h;
∵OA=MF=OC,∴S1=2a,同理可得S3=2b;
易知△OFC∽△NGE,则a:b=FC2:GE2=1:4,即b=4a;
∵a+b=
(S1+S3)=10,故a=2,b=8;
∴S△PCG=b=8;
梯形COHG中,PH=OC=FM=
CG=
PG,同上可证得S2=S△CPG;
所以S2=b=8,故选B.
 解:如图;(a、b分别表示△OFC、△GNE的面积)
解:如图;(a、b分别表示△OFC、△GNE的面积)∵F、G分别是BC、CE的中点,
∴△BMF、△OFC以及△CPG、△GNE都是全等的等边三角形;
∴S△CPG=b;
设M到AC的距离为h,则S1=OA•h,a=
| 1 |
| 2 |
∵OA=MF=OC,∴S1=2a,同理可得S3=2b;
易知△OFC∽△NGE,则a:b=FC2:GE2=1:4,即b=4a;
∵a+b=
| 1 |
| 2 |
∴S△PCG=b=8;
梯形COHG中,PH=OC=FM=
| 1 |
| 2 |
| 1 |
| 2 |
所以S2=b=8,故选B.
点评:此题主要考查了等边三角形、平行四边形的性质,相似三角形的性质及图形面积的求法;此题主要运用相似三角形的对应边成比例及面积比等于相似比的平方求解,能够发现△OFC、△GEN的面积之间的关系是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
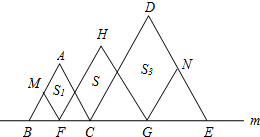 如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=
如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=
 若S1+S3=10,则S2=
若S1+S3=10,则S2=