题目内容
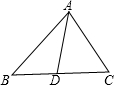已知：如图，D是BC上一点，AD平分∠BAC，AB=3cm，AC=2cm求：①S△ABD：S△ADC；②BD：CD．
分析：（1）作DE⊥AB于E，DF⊥AC于F，由角平分线的性质可知，DE=DF，再由三角形的面积公式求解即可；
（2）过A作AE⊥BC，垂足为E，由三角形的面积公式可得出
=
；
（2）过A作AE⊥BC，垂足为E，由三角形的面积公式可得出
| S△ABD |
| S△ACD |
| BD |
| DC |
解答：解：（1）如图：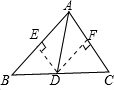
作DE⊥AB于E，DF⊥AC于F，∵AD是∠BAC的平分线，
∴DE=DF∴
=
=
=
；
（2）如图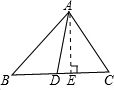
，过A作AE⊥BC，垂足为E，
∴S△ABD=
BD•AE，S△ACD=
DC•AE，
∴
=
由（1）的结论
=
，
∴
=
．
作DE⊥AB于E，DF⊥AC于F，∵AD是∠BAC的平分线，∴DE=DF∴
| S△ABD |
| S△ACD |
| ||
|
| AB |
| AC |
| 3 |
| 2 |
（2）如图
，过A作AE⊥BC，垂足为E，∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| S△ABD |
| S△ACD |
| BD |
| DC |
由（1）的结论
| S△ABD |
| S△ACD |
| AB |
| AC |
∴
| BD |
| CD |
| 3 |
| 2 |
点评：本题考查的是角平分线的性质及三角形的面积公式，由角平分线的性质及三角形的面积公式作出辅助线是解答此题的关键．
练习册系列答案
相关题目
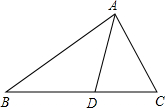已知：如图，D是BC上一点，AD平分∠BAC，AB=3，AC=2，若S△ABD=a，则S△ADC=
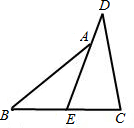22、阅读下面的题目及分析过程，并按要求进行证明．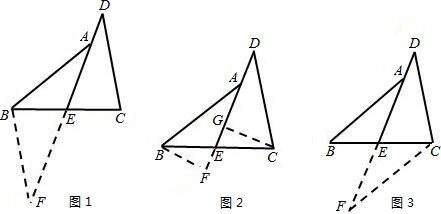
已知：如图，E是BC的中点，∠1=∠2，AE=DE．AB和DC相等吗？请说明理由．
已知：如图，AD是BC上的中线，且DF=DE．求证：△DBE≌△DCF．