题目内容
.已知:在平面直角坐标系中,抛物线![]() (
(![]() )交
)交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于点C,且对称轴为直线
轴于点C,且对称轴为直线![]() .
.
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是![]() 轴上的一个动点,请进行如下探究:
轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t?S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
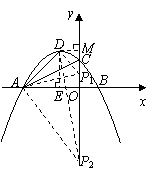
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
(参考资料:抛物线![]() 对称轴是直线
对称轴是直线![]()
![]() )
)
 |  | ||
解:(1)∵抛物线![]() (
(![]() )的对称轴为直线
)的对称轴为直线![]() .
.
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() .
.
(2)探究一:当![]() 时,
时,![]() 有最大值.
有最大值.
∵抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
当![]() 时,作
时,作![]() 轴于
轴于![]() ,
,
则![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]()
![]()
![]()
![]()
∴![]()
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() .
.
探究二:
 |
存在.分三种情况:
①当![]() 时,作
时,作![]() 轴于
轴于![]() ,则
,则![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
此时![]() ,又因为
,又因为![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴当![]() 时,存在点
时,存在点![]() ,使
,使![]() ,
,
此时![]() 点的坐标为(0,2).
点的坐标为(0,2).
②当![]() 时,则
时,则![]() ,
,
 |
∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() 与
与![]() 不相似,此时点
不相似,此时点![]() 不存在.
不存在.
③当![]() 时,以
时,以![]() 为直径作
为直径作![]() ,则
,则![]() 的半径
的半径![]() ,
,
圆心![]() 到
到![]() 轴的距离
轴的距离![]() .∵
.∵![]() ,∴
,∴![]() 与
与![]() 轴相离.
轴相离.
不存在点![]() ,使
,使![]() .
.
∴综上所述,只存在一点![]() 使
使![]() 与
与![]() 相似.
相似.

练习册系列答案
相关题目
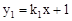 的图象与y轴交于点A,
的图象与y轴交于点A,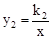 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐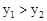 时x的取值范围。
时x的取值范围。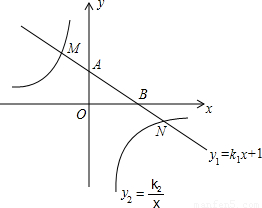
 ?
?