题目内容
直线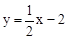 与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式;
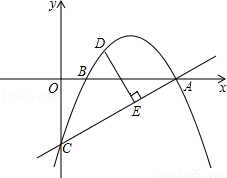
(2)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
解:(1)在直线解析式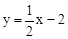 中,令x=0,得y=﹣2;令y=0,得x=4,
中,令x=0,得y=﹣2;令y=0,得x=4,
∴A(4,0),C(0,﹣2)。
设抛物线的解析式为y=ax2+bx+c,
∵点A(4,0),B(1,0),C(0,﹣2)在抛物线上,
∴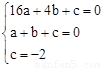 ,解得
,解得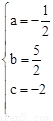 。
。
∴抛物线的解析式为: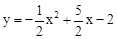 。
。
(2)设点D坐标为(x,y),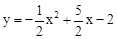 。
。
在Rt△AOC中,OA=4,OC=2,由勾股定理得:AC=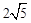 。
。
如图,连接CD、AD,过点D作DF⊥y轴于点F,过点A作AG⊥FD交FD的延长线于点G,
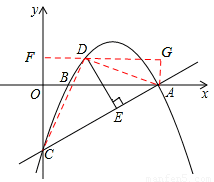
则FD=x,DG=4﹣x,OF=AG=y,FC=y+2。
S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG
=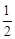 (AG+FC)•FG﹣
(AG+FC)•FG﹣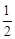 FC•FD﹣
FC•FD﹣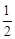 DG•AG
DG•AG
=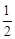 (y+y+2)×4﹣
(y+y+2)×4﹣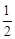 (y+2)•x﹣
(y+2)•x﹣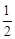 (4﹣x)•y
(4﹣x)•y
=2y﹣x﹣4
将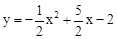 代入得:S△ACD=2y﹣x﹣4=﹣x2+4x=﹣(x﹣2)2+4。
代入得:S△ACD=2y﹣x﹣4=﹣x2+4x=﹣(x﹣2)2+4。
∴当x=2时,△ACD的面积最大,最大值为4。
当x=2时,y=1,∴D(2,1)。
∵S△ACD=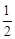 AC•DE,AC=
AC•DE,AC=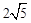 ,
,
∴当△ACD的面积最大时,高DE最大,
则DE的最大值为: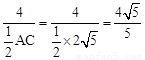 。
。
∴当D与直线AC的距离DE最大时,点D的坐标为(2,1),最大距离为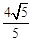 。
。
【解析】
试题分析:(1)首先求出点A,点C的坐标;然后利用待定系数法求出抛物线的解析式。
(2)AC为定值,当DE最大时,△ACD的面积最大,因此只需要求出△ACD面积的最大值即可。如图所示,作辅助线,利用S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG求出S△ACD的表达式,然后利用二次函数的性质求出最大值,并进而求出点D的坐标和DE的最大值。

 如图,直线
如图,直线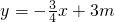 与x、y轴分别交于点A、B,以AB为直径的⊙M过原点O,垂直于x轴的直线MP与⊙M的下半圆交于点P.
与x、y轴分别交于点A、B,以AB为直径的⊙M过原点O,垂直于x轴的直线MP与⊙M的下半圆交于点P.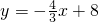 与x,y轴分别交于A、B两点,M是OB上
与x,y轴分别交于A、B两点,M是OB上 一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C.
一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C.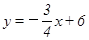 与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .
与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .
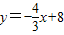 与x,y轴分别交于A、B两点,M是OB上一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C.
与x,y轴分别交于A、B两点,M是OB上一点,将△ABM沿AM折叠,点B恰好落在x轴上的点C.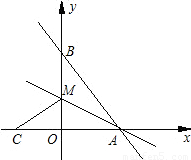
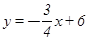 与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .
与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值: ▲ .