题目内容
【题目】解答
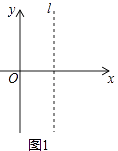
(1)观察与归纳:在如图1所示的平面直角坐标系中,直线l与y轴平行,点A与点B是直线l上的两点(点A在点B的上方).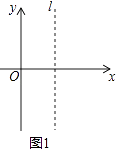
①小明发现:若点A坐标为(2,3),点B坐标为(2,﹣4),则AB的长度为;
②小明经过多次取l上的两点后,他归纳出这样的结论:若点A坐标为(t,m),点B坐标为(t,n),当m>n时,AB的长度可表示为;
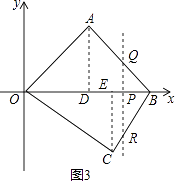
(2)如图2,正比例函数y=x与一次函数y=﹣x+6交于点A,点B是y=﹣x+6图象与x轴的交点,点C在第四象限,且OC=5.点P是线段OB上的一个动点(点P不与点O,B重合),过点P与y轴平行的直线l交线段AB于点Q,交射线OC于R,设点P横坐标为t,线段QR的长度为m.已知当t=4时,直线l恰好经过点C.
①求点A的坐标;
②求OC所在直线的关系式;
③求m关于t的函数关系式.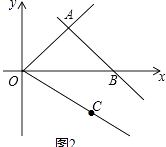
【答案】
(1)7;m﹣n
(2)
解:①解 ![]() 得
得 ![]() ,
,
∴A(3,3);
②∵直线l平行于y轴且当t=4时,直线l恰好过点C,如图2,作CE⊥OB于E,
∴OE=4,
在Rt△OCE中,OC=5,
由勾股定理得:
CE= ![]() =3,
=3,
∴点C的坐标为:(4,﹣3);
设OC所在直线的关系式为y=kx,则﹣3=4k,
∴k=﹣ ![]() ,
,
∴OC所在直线的关系式为y=﹣ ![]() x;
x;
③由直线y=﹣x+6可知B(6,0),
作AD⊥OB于D,
∵A(3,3),
∴OD=BD=AD=3,
∴∠AOB=45°,OA=AB,
∴∠OAB=90°,∠ABO=45°
当0<t≤3时,如图2,
∵直线l平行于y轴,
∴∠OPQ=90°,
∴∠OQP=45°,
∴OP=QP,
∵点P的横坐标为t,
∴OP=QP=t,
在Rt△OCE中,
∵tan∠EOC=|k|= ![]() ,
,
∴tan∠POR= ![]() =
= ![]() ,
,
∴PR=OPtan∠POR= ![]() t,
t,
∴QR=QP+PR=t+ ![]() t=
t= ![]() t,
t,
∴m关于t的函数关系式为:m= ![]() t;
t;
当3<t<6时,如图3,
∵∠BPQ=90°,∠ABO=45°,
∴∠BQP=∠PBQ=45°,
∴BP=QP,
∵点P的横坐标为t,
∴PB=QP=6﹣t,
∵PR∥CE,
∴△BPR∽△BEC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:PR=9﹣ ![]() t,
t,
∴QR=QP+PR=6﹣t+9﹣ ![]() t=15﹣
t=15﹣ ![]() t,
t,
∴m关于t的函数关系式为:m=15﹣ ![]() t;
t;
综上,m关于t的函数关系式为m= 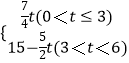

【解析】解:(1)①若点A坐标为(2,3),点B坐标为(2,﹣4),则AB的长度为3﹣(﹣4)=7;②若点A坐标为(t,m),点B坐标为(t,n),当m>n时,AB的长度可表示为m﹣n;
所以答案是7;m﹣n;
【考点精析】通过灵活运用正比例函数的图象和性质和一次函数的图象和性质,掌握正比函数图直线,经过一定过原点.K正一三负二四,变化趋势记心间.K正左低右边高,同大同小向爬山.K负左高右边低,一大另小下山峦;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案