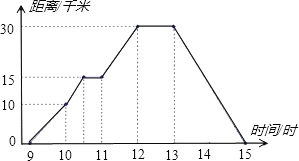
题目内容
【题目】如图,是井用手摇抽水机的示意图,支点A的左端是一手柄,右端是一弯钩,点F,A,B始终在同一直线上,支点A距离地面100cm,与手柄端点F之间的距离AF=50cm,与弯钩端点B之间的距离AB=10cm.KT为进水管.

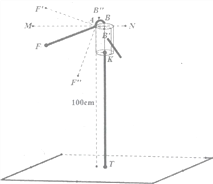
(1)在一次取水过程中,将手柄AF绕支点A旋转到AF′,且与水平线MN的夹角为20°,且此时点B′,K,T在一条线上,求点F′离地面的高度.
(2)当不取水时,将手柄绕支点A逆时针旋转90°至点F′′位置,求端点F′′与进水管KT之间的距离.(忽略进水管的粗细)(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
【答案】(1)117cm;(2)26.4cm.
【解析】分析:
(1)如下图,作F′G⊥MN,由题意可知,在Rt△AGF′中,∠GAF′=20°,AF′=AF=50,由此即可解得F′G的长度,由F′G+100即可求得所求的距离;
(2)如下图,作F″H⊥MN,B′L⊥MN,则由题意和(1)可得:AH=F′G=17,在∠F′′AH=90°-20°=70°,∠F′′AB′=90°,由此可得∠B′AL=20°,结合AB′=AB=10在Rt△ALB′中解得AL的长,再由AH+AL即可求得点所求的距离了.
详解:
(1)如下图,作F′G⊥MN,
∴∠F′GA=90°,
∴sin20°=![]() ,
,
又∵AF′=AF=50,
∴F′G=AF′×sin20°=50×0.34=17(cm),
∴点F′到地面的高度为17+100=117(cm).
(2)作F″H⊥MN,B′L⊥MN,
∴∠∠F′′AB′=∠ALB′=90°,
由题意得:∠F″AM=70°,∠F′′AB′=90°,
∴∠B′AL=20°,
∵AB′=AB=10,
∴AL=AB′·cos20°=9.4
又∵AH=F′G=17,
∴F″到水管KT的距离为17+9.4=26.4(cm).


【题目】观察下列图形,它是把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,将这种做法继续下去(如图2,图3…).观察规律解答以下各题:
 ……
……
(1)填写下表:
图形序号 | 挖去三角形的个数 |
图1 | 1 |
图2 | 1+3 |
图3 | 1+3+9 |
图4 |
(2)根据这个规律,求图n中挖去三角形的个数fn(用含n的代数式表示);
(3)若图n+1中挖去三角形的个数为fn+1,求fn+1-fn