��Ŀ����
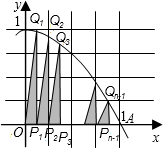
��ͼ����������y=-x2+1��ͼ����x������Ľ���ΪA�����߶�OA�ֳ�n�ȷݣ���ֵ�ֱ�ΪP1��P2����Pn-1����ÿ���ֵ���x��Ĵ��ߣ��ֱ��������߽��ڵ�Q1��Q2������Qn-1���ټ�ֱ��������OP1Q1��P1P2Q2������Pn-2Pn-1Qn-1������ֱ�ΪS1��S2��������������S1=
��S2=
��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ�������
| n2-1 |
| 2n3 |
| n2-4 |
| 2n3 |

A��
| ||
B��
| ||
C��
| ||
D��
|
��������֪��Pn����x�����ҽ��߶�OA�ֳ�n�ȷݣ���ÿ�ȷ�Ϊ
����Qn����������y=-x2+1�ϣ�������������ڵ׳��ԸߵĻ���
�����ô�ֱ��������ߣ��Ϳ���OP1Q1��P1P2Q2�����������ʾ�������ҳ����ɣ�д��Sm�ı���ʽ����ͣ����n�ܴ�ʱ�����W��ӽ��ij�����
| 1 |
| n |
| 1 |
| 2 |
����⣺��ͼ��֪S3=
���ܽ�����ɣ�Sm=
(1��m��n-1)��
��w=S1+S2+��+Sn-1=
+
+��+
=
=
=
=
-
-
+
-
=
-
-
��
��nԽ��Խ��ʱ����֪W��ӽ��ij���Ϊ
��
��ѡC��
| n2-9 |
| 2n3 |
| n2-m2 |
| 2n3 |
��w=S1+S2+��+Sn-1=
| n2-1 |
| 2n3 |
| n2-4 |
| 2n3 |
| n2-(n-1)2 |
| 2n3 |
| (n-1)n2-[1+22+��+(n-1)2] |
| 2n3 |
=
n3-n2-
| ||
| 2n3 |
=
| 4n3+3n2-7n |
| 12n3 |
=
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 6 |
| 1 |
| 4n |
| 1 |
| 12n2 |
=
| 1 |
| 3 |
| 1 |
| 4n |
| 1 |
| 12n2 |
��nԽ��Խ��ʱ����֪W��ӽ��ij���Ϊ
| 1 |
| 3 |
��ѡC��
���������⿼�����������ʺ������ʽ���ǵ������⣬Ҫ���ͼ��ͼ��ι�ϵ�����ͳһ����ʽSm��ѧ��۲�ͼ���������

��ϰ��ϵ�д�
�����Ŀ
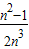 ��S2=
��S2=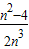 ��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��
��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��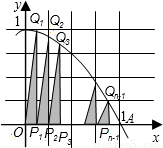




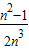 ��S2=
��S2=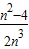 ��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��
��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��




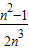 ��S2=
��S2=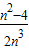 ��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��
��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��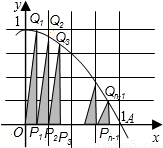




 ��S2=
��S2=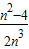 ��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��
��������W=S1+S2+��+Sn-1����nԽ��Խ��ʱ�������W��ӽ��ij����ǣ� ��



