Question

【题目】已知：二次函数y = ax2+ bx + c (a≠0)的图象如图所示，下列结论中：

①abc>0；②2a + b>0；③a +b＜m(am +b)(m≠1)；④(a+c)2< b2；⑤a >1．其中正确的项是( )

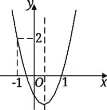
A.①②⑤B.①③④C.①②④D.②④⑤

Answer 1

【答案】A

【解析】

由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

解：①∵抛物线的开口向上，∴a＞0，

∵与y轴的交点为在y轴的负半轴上，∴c＜0，

∵对称轴为x=-＞0，

∴a、b异号，即b＜0，

又∵c＜0，∴abc＞0，

故结论①正确；

②∵对称轴为x=-＜1，a＞0，

∴-b＜2a，

∴2a+b＞0；

故结论②正确；

③当x=1时，y1=a+b+c；

当x=m时，y2=m(am+b)+c，当m＞1，y2＞y1；当m＜1，y2＜y1，所以不能确定；

故结论③错误；

④当x=1时，a+b+c=0；

当x=-1时，a-b+c＞0；

∴(a+b+c)(a-b+c)=0，即(a+c)2-b2=0，

∴(a+c)2=b2

故结论④错误；

⑤当x=-1时，a-b+c=2；

当x=1时，a+b+c=0，

∴a+c=1，

∴a=1+(-c)＞1，即a＞1；

故结论⑤正确；

综上所述，正确的是①②⑤．

故选：A．