Question

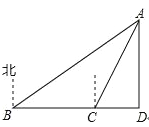
【题目】如图，一艘轮船航行到B处时，测得小岛A在船的北偏东60°的方向，轮船从B处继 续向正东方向航行200海里到达C处时，测得小岛A在船的北偏东30°的方向．己知在小岛周围170海里内有暗礁，若轮船不改变航向继续向前行驶，试问轮船有无触礁的危险？（≈1.732）

Answer 1

【答案】轮船不改变航向继续向前行使，轮船无触礁的危险．

【解析】

试题分析：如图，直角△ACD和直角△ABD有公共边AD，在两个直角三角形中，利用三角函数即可用AD表示出CD与BD，根据CB=BD-CD即可列方程，从而求得AD的长，与170海里比较，确定轮船继续向前行驶，有无触礁危险．

试题解析：该轮船不改变航向继续前行，没有触礁危险

理由如下：如图所示．

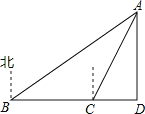
则有∠ABD=30°，∠ACD=60°．

∴∠CAB=∠ABD，

∴BC=AC=200海里．

在Rt△ACD中，设CD=x海里，

则AC=2x，AD=x，

在Rt△ABD中，AB=2AD=2x，

BD===3x，

又∵BD=BC+CD，

∴3x=200+x，

∴x=100．

∴AD=x=100≈173.2，

∵173.2海里＞170海里，

∴轮船不改变航向继续向前行使，轮船无触礁的危险．