题目内容
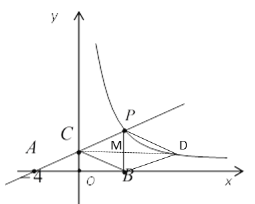
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 垂直
垂直![]() 轴于点
轴于点![]() ,且
,且![]() .
.
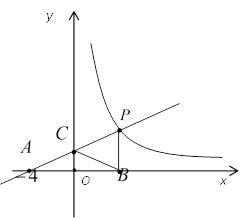
(1)仔细观察图形,直接写出![]() ;
;
(2)求![]() 和
和![]() 的值;
的值;
(3)在反比例函数图象上是否存在点![]() ,使四边形
,使四边形![]() 为平行四边形,如果存在,求出点
为平行四边形,如果存在,求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
【答案】(1)4;(2)![]() ;
;![]() ;(3)存在,点
;(3)存在,点![]()
【解析】
(1)由CA=CB求得B点坐标,然后根据PB⊥x轴,求出P点坐标,从而求解;
(2)分别将P点坐标代入一次函数和反比例函数解析式,求解;
(3)由题意得,D点只能在![]() 右侧,在反比例函数图像上取一点
右侧,在反比例函数图像上取一点![]() ,连接
,连接![]() 交PB于点M,要使得四边形
交PB于点M,要使得四边形![]() 是平行四边形,则要
是平行四边形,则要![]() 、CD互相平分,然后利用M点和C点坐标确定MC∥x轴,从而确定C点纵坐标,然后利用反比例函数解析式求得C点坐标,从而得到
、CD互相平分,然后利用M点和C点坐标确定MC∥x轴,从而确定C点纵坐标,然后利用反比例函数解析式求得C点坐标,从而得到![]() ,符合题意,问题得解.
,符合题意,问题得解.
解:(1)∵CA=CB,![]() ,
,
∴B(4,0)
又∵点![]() ,
,![]() 垂直
垂直![]() 轴于点
轴于点![]() ,
,
∴![]() ,即
,即![]()
故答案为:4
(2)将![]() 代入直线
代入直线![]() ,得
,得![]() ,解得:
,解得:![]() ;
;
![]() 代入反比例函数
代入反比例函数![]() ,得
,得![]() ,解得:
,解得:![]() ;
;
(3)由题意得,D点只能在![]() 右侧,在反比例函数图像上上取一点
右侧,在反比例函数图像上上取一点![]() ,连接
,连接![]() 交PB于点M
交PB于点M
要使得四边形![]() 是平行四边形,则须要
是平行四边形,则须要![]() 、CD互相平分
、CD互相平分
∴![]() ,
,
又∵在![]() 中,当x=0时,y=1
中,当x=0时,y=1
∴![]() ,即
,即![]() 轴,
轴,
∴设D(x,1),代入![]() 中,解得:x=8
中,解得:x=8
∴D(8,1),
此时![]()
∴存在点![]() 使四边形
使四边形![]() 为平行四边形.
为平行四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目