Question

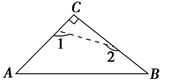
已知：如图，在菱形ABCD中，∠B= 60°，把一个含60°角的三角尺与这个菱形叠合，使三角尺60°角的顶点与点A重合，将三角尺绕点A按逆时针方向旋转 ．
(1)如图1，当三角尺的两边分别与菱形的两边BC、CD相交于点E、F．求证：CE+CF=AB；
(2)如图2，当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F．写出此时CE、CF、AB长度之间关系的结论．（不需要证明）

Answer 1

(1)证明见解析；（2）CF-CE=AB．

试题分析：（1）通过证明△ABE≌△ACF得出CF=BE,从而可证结论CE+CF=AB．
(2)可以通过证明△ACE≌△ADF，得出结论，由AB=AC、∠B=∠ACF，再利用等式的性质可得出∠BAE=∠CAF，从而利用AAS可证CE=DF，从而CF-CE=AB．
试题解析：在△ABE和△ACF中，
∵∠BAE+∠EAC=∠CAF+∠EAC=60°，
∴∠BAE=∠CAF．
∵AB=AC，∠B=∠ACF=60°，
∴△ABE≌△ACF（ASA）．
∴BE=CF；
∴CF+CE=BE+CE=BC=AB;
(2) CF-CE=AB．