题目内容
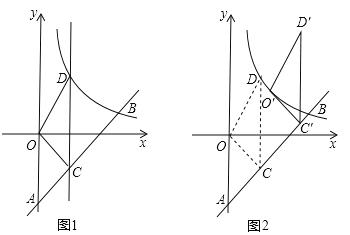
【题目】如图,已知抛物线y=ax+![]() x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
(1)求出A点的坐标、B点坐标;
(2)求出直线BC的解析式;
(3)点Q是直线BC上方的抛物线上的一动点(不与B、C重合),是否存在点Q,使△QBC的面积最大.若存在,请求出△QBC的最大面积,若不存在,试说明理由;
(4)若E在x轴上,点F在抛物线上,以A、C、E、F为顶点的四边形是平行四边形时,请直接写出点E的坐标。
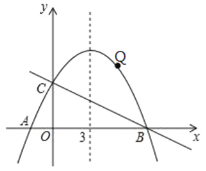
【答案】(1) A(﹣2,0),B(8,0);(2) y=﹣![]() x+4;(3)见解析;(4) E的坐标为(﹣8,0),(4,0),(5+
x+4;(3)见解析;(4) E的坐标为(﹣8,0),(4,0),(5+![]() ,0),(5﹣
,0),(5﹣![]() ,0).
,0).
【解析】
(1)由抛物线的对称轴为直线x=3,利用二次函数的性质即可求出a值,进而可得出抛物线的解析式,再利用二次函数图象上点的坐标特征,即可求出点A、B的坐标;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,由点B、C的坐标,利用待定系数法即可求出直线BC的解析式,
(3)假设存在,设点Q的坐标为(x,-![]() x2+
x2+![]() x+4),过点Q作QD∥y轴,交直线BC于点D,则点D的坐标为(x,-
x+4),过点Q作QD∥y轴,交直线BC于点D,则点D的坐标为(x,-![]() x+4),QD=-
x+4),QD=-![]() x2+2x,利用三角形的面积公式即可得出S△QBC关于x的函数关系式,再利用二次函数的性质即可解决最值问题;
x2+2x,利用三角形的面积公式即可得出S△QBC关于x的函数关系式,再利用二次函数的性质即可解决最值问题;
(4)有四种情形,利用平行四边形的性质可得点F的纵坐标的绝对值为-4,求出等F的坐标即可解决问题;
解:(1)∵抛物线y=ax2+![]() x+4的对称轴是直线x=3,
x+4的对称轴是直线x=3,
∴﹣![]() =3,解得:a=﹣
=3,解得:a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4.
x+4.
当y=0时,﹣![]() x2+
x2+![]() x+4=0,
x+4=0,
解得:x1=﹣2,x2=8,
∴点A的坐标为(﹣2,0),点B的坐标为(8,0).
故答案为(﹣2,0),(8,0).
(2)当x=0时,y=4,
∴点C的坐标为(0,4).
设直线BC的解析式为y=kx+b(k≠0).
将B(8,0)、C(0,4)代入y=kx+b,
![]() ,解得:
,解得: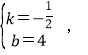
∴直线BC的解析式为y=﹣![]() x+4.
x+4.
故答案为y=﹣![]() x+4.
x+4.
(3)假设存在,设点Q的坐标为(x,﹣![]() x2+
x2+![]() x+4),过点Q作QD∥y轴,交直线BC于点D,则点D的坐标为(x,﹣
x+4),过点Q作QD∥y轴,交直线BC于点D,则点D的坐标为(x,﹣![]() x+4),如图所示.
x+4),如图所示.
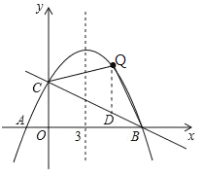
∴QD=﹣![]() x2+
x2+![]() x+4﹣(﹣
x+4﹣(﹣![]() x+4)=﹣
x+4)=﹣![]() x2+2x,
x2+2x,
∴S△QBC=![]() QDOB=
QDOB=![]() ×8(﹣
×8(﹣![]() x2+2x)=﹣x2+8x=﹣(x﹣4)2+16.
x2+2x)=﹣x2+8x=﹣(x﹣4)2+16.
∵﹣1<0,
∴当x=4时,△QBC的面积最大,最大面积是16.
∵0<x<8,
∴存在点Q,使△QBC的面积最大,最大面积是16.
(4)满足条件的点E的坐标为(﹣8,0),(4,0),(5+![]() ,0),(5﹣
,0),(5﹣![]() ,0).
,0).
如图,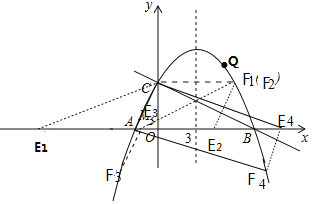
当AC为平行四边形的边时,点N的纵坐标的绝对值为4,
可得F1(F2)(6,4),E2(4,0),
F3(3-![]() ,-4),F4(3+
,-4),F4(3+![]() ,-4),可得E3(5-
,-4),可得E3(5-![]() ,0),E4
,0),E4![]() ,0),
,0),
当AC为对角线时,可得E1(-8,0),
综上所述,满足条件的点E的坐标为(-8,0),(4,0),(5+![]() ,0),(5-
,0),(5-![]() ,0).
,0).