��Ŀ����
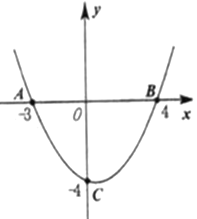
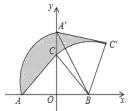
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y��kx+b��k��0����ͼ���뷴��������y��![]() ��n��0����ͼ���ڵڶ����������ڵ�A��B������x�ύ�ڵ�C����B����Ϊ��m����1����AD��x�ᣬ��AD��3��tan��AOD��
��n��0����ͼ���ڵڶ����������ڵ�A��B������x�ύ�ڵ�C����B����Ϊ��m����1����AD��x�ᣬ��AD��3��tan��AOD��![]()
��1����÷�����������һ�κ����Ľ���ʽ��
��2������OB����S��AOC��S��BOC��ֵ��
��3����E��x����һ�㣬����AOE�ǵ�����������ֱ��д������������E��ĸ�����д���������ɣ��������E�����꣩��
���𰸡���1��y����![]() ��y����
��y����![]() x+2����2��S��AOC��S��BOC��4����3�����������ĵ�P���ĸ���
x+2����2��S��AOC��S��BOC��4����3�����������ĵ�P���ĸ���
��������
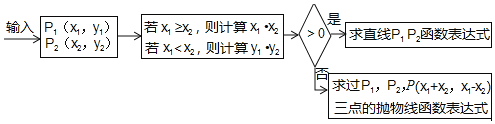
��1���ȸ���������Ǻ������OD�������A���꣬���������������������ʽ���������B���꣬���A��B�������ֱ�߽���ʽ�У����ɵó����ۣ�
��2���������C���꣬�����������ε������ʽ��⼴�ɵó����ۣ�
��3����������������õ��������ε����ʣ�����������⼴�ɵó����ۣ�
��1����AD��x�ᣬ
���ADO��90����
��Rt��ADO��AD��3��tan��AOD��![]() ��
��
��OD��2��
��A����2��3����
�ߵ�A�ڷ���������y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��n����2��3����6��
�෴���������Ľ���ʽΪy����![]() ��
��
�ߵ�B��m����1���ڷ���������y����![]() ��ͼ���ϣ�
��ͼ���ϣ�
�ੁm����6��
��m��6��
��B��6����1����
����A����2��3����B��6����1������ֱ��y��kx+b�У���![]() ��
��
�� ��
��
��һ�κ����Ľ���ʽΪy����![]() x+2��
x+2��
��2���ɣ�1��֪��A����2��3����ֱ��AB�Ľ���ʽΪy����![]() x+2��
x+2��
��y��0��
�ੁx+2��0��
��x��4��
��C��4��0����
��S��AOC��S��BOC��![]() OC|yA|��
OC|yA|��![]() OC|yB|��
OC|yB|��![]() ��4��3��1����4��
��4��3��1����4��
��3����E��m��0�����ɣ�1��֪��A����2��3����
��OA2��13��OE2��m2��AE2����m+2��2+9��
�ߡ�AOE�ǵ��������Σ�
��ٵ�OA��OEʱ��
��13��m2��
p>��m������E����![]() ��0����
��0����![]() ��0����
��0����
�ڵ�OA��AEʱ��13����m+2��2+9��
��m��0���ᣩ��m��4��
��E��4��0����
�۵�OE��AEʱ��m2����m+2��2+9��
��m����![]() ��
��
��E����![]() ��0����
��0����
�������������ĵ�P���ĸ���

 �������ϵ�д�
�������ϵ�д�����Ŀ��С������A��B������Ʒ��ÿ�ι���ͬһ����Ʒ�ĵ�����ͬ��������Ϣ���±���
���� | ������������ | �����ܷ��ã�Ԫ | |
A | B | ||
��һ�� | 2 | 1 | 55 |
�ڶ��� | 1 | 3 | 65 |
����������Ϣ����������⣺
��1����A��B������Ʒ�ĵ��ۣ�
��2���������ι�����������Ʒ��12������A����Ʒ������������B����Ʒ������2��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�