题目内容
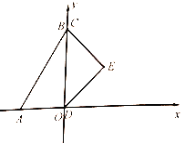
【题目】如图，一段圆弧与长度为1的正方形网格的交点是A、B、C．
(1)请完成以下操作：
①以点O为原点，垂直和水平方向为轴，网格边长为单位长，建立平面直角坐标系；
②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD；
(2)请在(1)的基础上，完成下列填空：⊙D的半径为__________；点（6，–2）在⊙D__________；（填“上”、“内”、“外”）∠ADC的度数为__________．
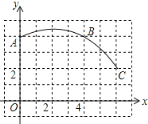
【答案】（1）①见解析；②见解析；（2）2
；上；90°；
【解析】
（1）根据图形和垂径定理画出图形即可；
（2）根据勾股定理求出半径即可；根据点到圆心的距离即可得到结论；
③证△AOD≌△DFC，根据全等得出∠OAD=∠CDF，即可求出答案．
（1）①平面直角坐标系如图所示：
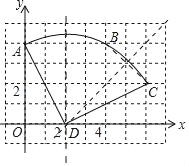
②圆心点D，如图所示；
（2）⊙D的半径=AD=
，
∵点（6，﹣2）到圆心D的距离==半径，
∴点（6，﹣2）在⊙D上．
观察图象可知：∠ADC=90°.
练习册系列答案
全优点练单元计划系列答案
相关题目
