题目内容
已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.

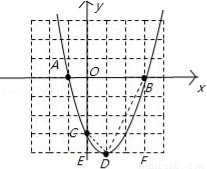
(1)求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.
【答案】
(1)A(﹣1,0),B(3,0),C(0,﹣3),D(1,﹣4)图形见解析;
(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;
(3)四边形OCDB的面积为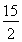 .
.
【解析】
试题分析:(1)先把此二次函数化为y=(x+1)(x﹣3)的形式,即可求出A、B两点的坐标,由二次函数的解析式可知c=﹣3,故可知C点坐标,由二次函数的顶点式即可求出其顶点坐标;
(2)根据四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED即可解答.
试题解析:(1)∵二次函数y=x2﹣2x﹣3可化为y=(x+1)(x﹣3),A在B的左侧,
∴A(﹣1,0),B(3,0),
∵c=﹣3,
∴C(0,﹣3),
∵x=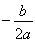 =
=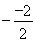 =1,y=
=1,y=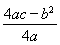 =﹣4,
=﹣4,
∴D(1,﹣4),故此函数的大致图象为:
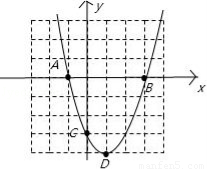
(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;
(3)连接CD、BD,
则四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED
=OB•|OE|﹣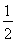 DF•|BF|﹣
DF•|BF|﹣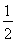 DE•CE
DE•CE
=3×4﹣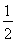 ×2×4﹣
×2×4﹣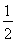 ×1×1
×1×1
=12﹣4﹣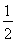
=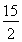 .
.
 .
.
考点:二次函数图象上点的坐标特征.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目