题目内容
【题目】如图，抛物线y=﹣x2+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D．下列四个命题：①当x＞0时，y＞0； ②若a=﹣1，则b=3；③抛物线上有两点P（x1 ， y1）和Q（x2 ， y2），若x1＜1＜x2 ， 且x1+x2＞2，则y1＞y2；④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为6 
．其中正确的命题有（ ）个．
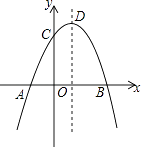
A.1
B.2
C.3
D.4
【答案】B
【解析】解：①当x＞0时，函数图象过一四象限，当0＜x＜b时，y＞0；当x＞b时，y＜0，故本选项错误；②二次函数对称轴为x=﹣ 
=1，当a=﹣1时有 
=1，解得b=3，故本选项正确；③∵x1+x2＞2，
∴ 
＞1，
又∵x1﹣1＜1＜x2﹣1，
∴Q点距离对称轴较远，
∴y1＞y2，故本选项正确；④如图，作D关于y轴的对称点D′，E关于x轴的对称点E′，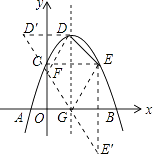 
连接D′E′，D′E′与DE的和即为四边形EDFG周长的最小值．
当m=2时，二次函数为y=﹣x2+2x+3，顶点纵坐标为y=﹣1+2+3=4，D为（1，4），则D′为（﹣1，4）；C点坐标为C（0，3）；则E为（2，3），E′为（2，﹣3）；
则DE= 
= 
；D′E′= 
= 
；
∴四边形EDFG周长的最小值为 + ，故本选项错误．
正确的有2个．
所以答案是：B．
【考点精析】根据题目的已知条件，利用抛物线与坐标轴的交点的相关知识可以得到问题的答案，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
