题目内容
25、三等分任意角是一个作图难题，在距第一次提出这个问题两千年之后，这个问题才被证实用尺规作图（用没有刻度的直尺和圆规作图）无法解决．现在有不少人创造了各种各样的辅助工具，用来解决尺规作图无法解决的三等分任意角的问题．
如图所示就是一个用来三等分任意角的工具及其使用示意图．
（1）制作该工具时BE所在的直线、点C应分别满足什么条件？使用时应注意些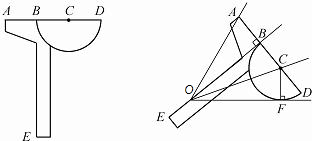
什么？
（2）你能说出该工具三等分任意角的道理吗？
如图所示就是一个用来三等分任意角的工具及其使用示意图．
（1）制作该工具时BE所在的直线、点C应分别满足什么条件？使用时应注意些
什么？（2）你能说出该工具三等分任意角的道理吗？
分析：（1）由线段垂直平分线的性质，角平分线的性质可知，BE垂直平分AC，点C为半圆的圆心；
（2）根据垂直平分线的点到线段两端点距离相等，构造等腰三角形，根据等腰三角形的性质可知EB为角平分线，由圆的性质可知CB=CF，可知C在角平分线上．
（2）根据垂直平分线的点到线段两端点距离相等，构造等腰三角形，根据等腰三角形的性质可知EB为角平分线，由圆的性质可知CB=CF，可知C在角平分线上．
解答：（1）BE垂直平分AC，C是BD的中点；角的顶点落在BE上，使角的一边经过点A，另一边于半圆相切．（3′）
（2）如图，设被平分的角顶点为O点，
∵BE垂直平分AC，∴OA=OC，∴∠AOB=∠BOC，
∵C是BD的中点，∴CB=CF，且BC⊥OB，CF⊥OF，
∴∠BOC=∠FOC，
∴该工具能三等分任意角．
（2）如图，设被平分的角顶点为O点，
∵BE垂直平分AC，∴OA=OC，∴∠AOB=∠BOC，
∵C是BD的中点，∴CB=CF，且BC⊥OB，CF⊥OF，
∴∠BOC=∠FOC，
∴该工具能三等分任意角．
点评：本题考查了线段垂直平分线的性质，角平分线性质的运用．关键是运用两个性质得到相等角．
练习册系列答案
相关题目
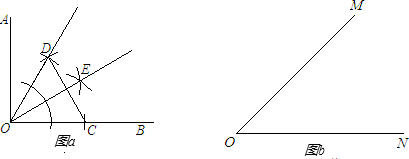
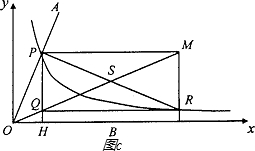
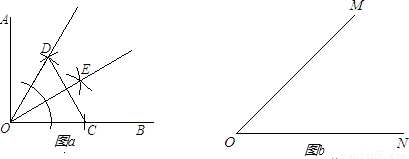
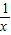的图象交于点P，以P为圆心、2OP长为半径作弧交图象于点R．分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=
∠AOB．要明白帕普斯的方法，请研究以下问题：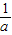
）、R（b，
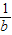），求直线OM对应的函数关系式（用含a、b的代数式表示）．
∠AOB．
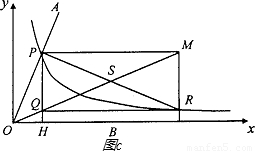
∠MCN．这种方法由于在直尺上作了一个记号，不符合尺规作图中直尺只能用来连线的规定，因此还不能算是严格意义上的尺规作图．
∠MCN．这种方法由于在直尺上作了一个记号，不符合尺规作图中直尺只能用来连线的规定，因此还不能算是严格意义上的尺规作图．