题目内容
在复习《反比例函数》一课时,同桌的小明和小芳有一个问题观点不一致.小明认为如果两次分别从1~6六个整数中任取一个数,第一个数作为点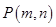 的横坐标,第二个数作为点
的横坐标,第二个数作为点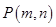 的纵坐标,则点
的纵坐标,则点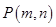 在反比例函数
在反比例函数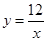 的图象上的概率一定大于在反比例函数
的图象上的概率一定大于在反比例函数 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
小题1:试用列表或画树状图的方法列举出所有点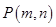 的情形;
的情形;
小题2:分别求出点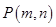 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
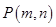 的横坐标,第二个数作为点
的横坐标,第二个数作为点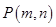 的纵坐标,则点
的纵坐标,则点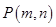 在反比例函数
在反比例函数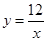 的图象上的概率一定大于在反比例函数
的图象上的概率一定大于在反比例函数 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?小题1:试用列表或画树状图的方法列举出所有点
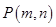 的情形;
的情形;小题2:分别求出点
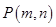 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.小题1:列表如下

| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1 | (1,1 ) | (1,2 ) | (1,3 ) | (1,4 ) | (1,5 ) | (1,6) | ||||
| 2 | (2,1 ) | (2,2 ) | (2,3 ) | (2,4 ) | (2,5 ) | (2,6) | ||||
| 3 | (3,1 ) | (3,2 ) | (3,3 ) | (3,4 ) | (3,5 ) | (3,6) | ||||
| 4 | (4,1 ) | (4,2 ) | (4,3 ) | (4,4 ) | (4,5 ) | (4,6) | ||||
| 5 | (5,1) | (5,2) | (5,3 ) | (5,4 ) | (5,5 ) | (5,6) | ||||
| 6 | (6,1 ) | (6,2) | (6,3 ) | (6,4 ) | (6,5 ) | (6,6) |
小题2:
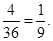 小芳的观点正确
小芳的观点正确(1)列表如下:
或画树状图如下: 
(2)由树状图或表格可知,点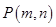 共有36种可能的结果,且每种结果出现的可能性相同,点(3,4),(4,3),(2,6),(6,2)在反比例函数
共有36种可能的结果,且每种结果出现的可能性相同,点(3,4),(4,3),(2,6),(6,2)在反比例函数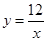 的图象上,
的图象上,
点 (2,3),(3,2),(1,6),(6,1)在反比例函数 的图象上,
的图象上,
故点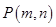 在反比例函数
在反比例函数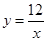 和
和 的图象上的概率相同,都是
的图象上的概率相同,都是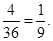
所以小芳的观点正确.

| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1 | (1,1 ) | (1,2 ) | (1,3 ) | (1,4 ) | (1,5 ) | (1,6) | ||||
| 2 | (2,1 ) | (2,2 ) | (2,3 ) | (2,4 ) | (2,5 ) | (2,6) | ||||
| 3 | (3,1 ) | (3,2 ) | (3,3 ) | (3,4 ) | (3,5 ) | (3,6) | ||||
| 4 | (4,1 ) | (4,2 ) | (4,3 ) | (4,4 ) | (4,5 ) | (4,6) | ||||
| 5 | (5,1) | (5,2) | (5,3 ) | (5,4 ) | (5,5 ) | (5,6) | ||||
| 6 | (6,1 ) | (6,2) | (6,3 ) | (6,4 ) | (6,5 ) | (6,6) |

(2)由树状图或表格可知,点
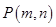 共有36种可能的结果,且每种结果出现的可能性相同,点(3,4),(4,3),(2,6),(6,2)在反比例函数
共有36种可能的结果,且每种结果出现的可能性相同,点(3,4),(4,3),(2,6),(6,2)在反比例函数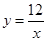 的图象上,
的图象上,点 (2,3),(3,2),(1,6),(6,1)在反比例函数
 的图象上,
的图象上, 故点
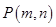 在反比例函数
在反比例函数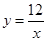 和
和 的图象上的概率相同,都是
的图象上的概率相同,都是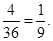
所以小芳的观点正确.

练习册系列答案
相关题目
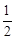 ;
;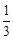 ;
;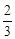 ;
; .
.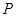 的横坐标,再将小球放回搅匀,又从中拿出一个,将该小球上的数字作为点
的横坐标,再将小球放回搅匀,又从中拿出一个,将该小球上的数字作为点 与直线
与直线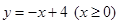 和
和 轴所围成的三角形内(含三角形边界)的概率为 。
轴所围成的三角形内(含三角形边界)的概率为 。