题目内容
 如图,将等腰直角△ABC(∠ACB=90°,AC=BC)绕C点按逆时针方向旋转到△A'CB'的位置,若∠A'+∠A'CB=170°,则∠ACB'等于
如图,将等腰直角△ABC(∠ACB=90°,AC=BC)绕C点按逆时针方向旋转到△A'CB'的位置,若∠A'+∠A'CB=170°,则∠ACB'等于
- A.35°
- B.45°
- C.55°
- D.65°
C
分析:由题意可知,等腰直角△ABC中,∠A=45°,∠ACB=90°,根据旋转的性质得,∠A'=45°,∠A'CB′=90°,由∠A'+∠A'CB=170°,可得,∠A'+∠A'CA+∠ACB=170°,得∠A'CA=35°,即可求出结论;
解答:∵△ABC是等腰直角三角形,
∴∠A=45°,∠ACB=90°,
根据旋转的性质得,∠A'=45°,∠A'CB′=90°,
∵∠A'+∠A'CB=170°,
∴∠A'+∠A'CA+∠ACB=170°,
得∠A'CA=170°-45°-90°=35°,
∴∠ACB'=∠A'CB′-∠A'CA,
=90°-35°,
=55°;
故选C.
点评:本题考查了等腰三角形的性质及旋转的性质,①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
分析:由题意可知,等腰直角△ABC中,∠A=45°,∠ACB=90°,根据旋转的性质得,∠A'=45°,∠A'CB′=90°,由∠A'+∠A'CB=170°,可得,∠A'+∠A'CA+∠ACB=170°,得∠A'CA=35°,即可求出结论;
解答:∵△ABC是等腰直角三角形,
∴∠A=45°,∠ACB=90°,
根据旋转的性质得,∠A'=45°,∠A'CB′=90°,
∵∠A'+∠A'CB=170°,
∴∠A'+∠A'CA+∠ACB=170°,
得∠A'CA=170°-45°-90°=35°,
∴∠ACB'=∠A'CB′-∠A'CA,
=90°-35°,
=55°;
故选C.
点评:本题考查了等腰三角形的性质及旋转的性质,①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
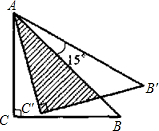 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
 如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若BC=3
如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若BC=3 如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为
如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为 如图,将等腰直角△ABC(∠ACB=90°,AC=BC)绕C点按逆时针方向旋转到△A'CB'的位置,若∠A'+∠A'CB=170°,则∠ACB'等于( )
如图,将等腰直角△ABC(∠ACB=90°,AC=BC)绕C点按逆时针方向旋转到△A'CB'的位置,若∠A'+∠A'CB=170°,则∠ACB'等于( ) 如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1,若BC=
如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1,若BC=