Question

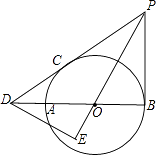
【题目】如图，Rt△ABC中，AB=AC，∠BAC=90°，BE⊥CE，垂足是E，BE交AC于点D，F是BE上一点，AF⊥AE，且C是线段AF的垂直平分线上的点，AF=2，则DF=________.

Answer 1

【答案】3.

【解析】

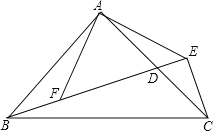
由题意可证的△ABF≌△ACE,可得△AEF为等腰直角三角形，取AF的中点O，连接CO交BE与点G，连接AG，可得△AGF, △AGE,△CEG均为等腰直角三角形，可得AG平行等于CE，可得四边形AGCE为平行四边形，可得FD的长.

解：如图

Rt△ABC中，AB=AC，∠BAC=90°，∠ABC=∠ACB=45°，

又∠BAC=90°，BE⊥CE，∠DAE为∠BAC与EAF的公共角

∠BAF=∠CAE,

∠ABC=∠ACB=45°, BE⊥CE

∠ABF+∠CBE=45°,∠CBE+∠ACB+∠ACE=90°,即: ∠CBE+∠ACE=45°，

∠ABF=∠ACE，

在△ABF与△ACE中，有

，△ABF≌△ACE，

AE=AF, △AEF为等腰直角三角形, 取AF的中点O，连接CO交BE与点G，连接AG,

C是线段AF的垂直平分线上的点，易得△AGF, △AGE,△CEG均为等腰直角三角形，

AF=2 AG=GE=CE=FG=2,

又AG⊥BE,CE⊥BE,可得AG∥CE,

四边形AGCE为平行四边形，

GD=DE=1,

DF=FG+GD=2+1=3.