题目内容
【题目】如图,四边形ABCD中,∠A=∠B=90°,AB=25,AD=15,BC=10,点E是AB上一点,且DE=CE,求AE的长. 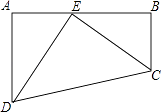
【答案】解:设AE=x, ∵AB=25,
∴BE=25﹣x,
∵∠A=∠B=90°,
∴DE2=AD2+AE2=152+x2 ,
CE2=BC2+BE2=102+(25﹣x)2 ,
∵DE=CE,
∴152+x2=102+(25﹣x)2 ,
解得x=10,
所以,AE=10.
【解析】设AE=x,表示出BE=25﹣x,再分别利用勾股定理列式表示出DE2、CE2 , 然后根据DE=CE列方程求解即可.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目