题目内容
为尽快了解浦东新区在一次教学质量测试中初三19 000名学生数学成绩的基本情况,从中随机抽取300名学生的数学成绩,通过数据整理计算,得频率分布表.(注:原始成绩均为整数,分数段中的成绩可含最低值,不含最高值)(1)将未完成的3个数据直接填入表内空格中;
(2)这300名学生数学成绩的中位数落在分数段______中;
(3)在这次考试中,估计浦东新区19 000名初三学生的数学成绩在80分及80分以上的人数约为______名.
| 分数段 | 频数 | 频率 |
| 0~60 | 27 | 0.09 |
| 60~70 | 39 | |
| 70~80 | 75 | 0.25 |
| 80~90 | ||
| 90~101 | 63 | 0.21 |
【答案】分析:(1)因为抽查的人数是300,根据里面的频数和频率可填空.
(2)中位数就是本组数据按照从小到大排列位于中间位置的数,所以可找到落在哪组数据内.
(3)求出80分及80分以上的人数所占的百分比乘以总人数即可.
解答:解:(1)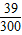 =0.13;300-27-39-75-63=96;
=0.13;300-27-39-75-63=96;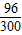 =0.32.(每格(2分),共6分)
=0.32.(每格(2分),共6分)
(2)中位数在80~90内.(2分)
(3)19000×(0.21+0.32)=10070.数学成绩在80分及80分以上的人数约为10070人.
(2分)
点评:本题考查了频率分布表,知道频率= ,以及用样本估计总体和中位数的概念.
,以及用样本估计总体和中位数的概念.
(2)中位数就是本组数据按照从小到大排列位于中间位置的数,所以可找到落在哪组数据内.
(3)求出80分及80分以上的人数所占的百分比乘以总人数即可.
解答:解:(1)
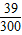 =0.13;300-27-39-75-63=96;
=0.13;300-27-39-75-63=96;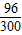 =0.32.(每格(2分),共6分)
=0.32.(每格(2分),共6分)(2)中位数在80~90内.(2分)
(3)19000×(0.21+0.32)=10070.数学成绩在80分及80分以上的人数约为10070人.
(2分)
点评:本题考查了频率分布表,知道频率=
 ,以及用样本估计总体和中位数的概念.
,以及用样本估计总体和中位数的概念. 
练习册系列答案
相关题目
为尽快了解浦东新区在一次教学质量测试中初三19 000名学生数学成绩的基本情况,从中随机抽取300名学生的数学成绩,通过数据整理计算,得频率分布表.(注:原始成绩均为整数,分数段中的成绩可含最低值,不含最高值)
(1)将未完成的3个数据直接填入表内空格中;
(2)这300名学生数学成绩的中位数落在分数段 中;
(3)在这次考试中,估计浦东新区19 000名初三学生的数学成绩在80分及80分以上的人数约为 名.
(1)将未完成的3个数据直接填入表内空格中;
(2)这300名学生数学成绩的中位数落在分数段
(3)在这次考试中,估计浦东新区19 000名初三学生的数学成绩在80分及80分以上的人数约为
| 分数段 | 频数 | 频率 |
| 0~60 | 27 | 0.09 |
| 60~70 | 39 | |
| 70~80 | 75 | 0.25 |
| 80~90 | ||
| 90~101 | 63 | 0.21 |