题目内容
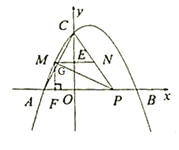
【题目】如图,已知抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
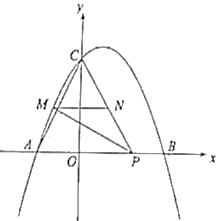
(1)点A的坐标为_____,点C的坐标为______;
(2)如图,点M在抛物线![]() 位于A、C两点间的部分(与A、C两点不重合),过点M作PM⊥AC,与x轴正半轴交于点P,连接PC,过点M作MN平行于x轴,交PC于点N.
位于A、C两点间的部分(与A、C两点不重合),过点M作PM⊥AC,与x轴正半轴交于点P,连接PC,过点M作MN平行于x轴,交PC于点N.
①若点N为PC的中点,求出PM的长;
②当MN=NP时,求PC的长以及点M的坐标.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②PC=5,点
,②PC=5,点![]() 的坐标为
的坐标为![]()
【解析】
(1)在抛物线的解析式中,分别令y=0和x=0,即可得出结论.
(2)设直线MN与y轴相交于点E.过M作MF⊥x轴,垂足为F.
①由N是CP的中点,MN平行于x轴,得到E为CO的中点,从而得出MF =2,令抛物线解析式中y=2,解方程即可得出M的坐标,易求直线AC的解析式为y=2x+4,,由MP⊥AC,可设直线MP为![]() ,把M的坐标代入得到b的值,从而得到直线MP的解析式,进而求出P的坐标,根据两点间的距离公式即可求出PM的值.
,把M的坐标代入得到b的值,从而得到直线MP的解析式,进而求出P的坐标,根据两点间的距离公式即可求出PM的值.
②设AC交MP于G.由平行线的性质和等腰三角形的性质可得∠NPM=∠MPA,进而得到△APG≌△CPG,根据全等三角形的性质得到AG=GC,AP=PC.设P(x,0),根据两点间的距离公式列方程,求出x的值,可得P的坐标,得到PC=PA=5.再由中点坐标公式得到G的坐标.求出直线PG的解析式,和抛物线的解析式联立组成方程组,解方程组即可得到M的坐标.
(1)在![]() 中,令y=0,得:
中,令y=0,得:![]() ,解得:x=-2或x=4,∴A(-2,0),B(4,0).令x=0,得:y=4,∴C(0,4).
,解得:x=-2或x=4,∴A(-2,0),B(4,0).令x=0,得:y=4,∴C(0,4).
(2)直线MN与y轴相交于点E.过M作MF⊥x轴,垂足为F.
①∵N是CP的中点,MN平行于x轴,∴E为CO的中点,∴MF=OE=![]() CO=2,∴
CO=2,∴![]() ,解得:x=
,解得:x=![]() 或x=
或x=![]() (舍去),∴M(
(舍去),∴M(![]() ,2),易求直线AC的解析式为y=2x+4.
,2),易求直线AC的解析式为y=2x+4.
∵MP⊥AC,∴直线MP为![]() ,把M(
,把M(![]() ,2)代入得:b=
,2)代入得:b=![]() ,∴直线MP的解析式为:
,∴直线MP的解析式为:![]() ,令y=0,得:x=
,令y=0,得:x=![]() ,∴P(
,∴P(![]() ,0),∴PM=
,0),∴PM=![]() .
.
②设AC交MP于G.
∵MN∥AB,∴∠NMP=∠MPA.
∵MN=NP,∴∠NMP=∠NPM,∴∠NPM=∠MPA.
∵PG=PG,∠PGA=∠PGC=90°,∴△APG≌△CPG,∴AG=GC,AP=PC.设P(x,0),∴![]() ,解得:x=3,∴P(3,0),∴PC=PA=3+2=5.
,解得:x=3,∴P(3,0),∴PC=PA=3+2=5.
∵AG=GC,∴G为AC的中点,∴G(-1,2).
设直线PG为y=kx+b,∴![]() ,解得:
,解得: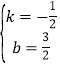 ,∴直线PG为
,∴直线PG为![]() .解方程组:
.解方程组: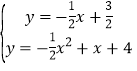 ,得:
,得: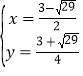 或
或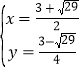 (舍去),∴点M的坐标为
(舍去),∴点M的坐标为![]() .
.