题目内容
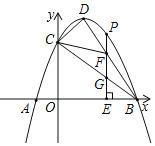
已知如图,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=120°,∠2=60°,求证AB∥CD;
(2)在(1)的情况下,若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系;
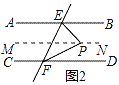
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式)
【解析】
如图2,过点P作MN∥AB,
则∠EPM=∠PEB_____.
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD_____.
∴∠MPF=∠PFD
∴∠_____+∠_____=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD
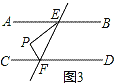
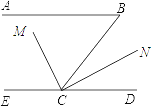
②当点P在图3的位置时,∠EPF、∠PEB、∠PFD三个角之间有何关系并证明.
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系:_____.


练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目





 有实数根,则k的取值范围是
有实数根,则k的取值范围是

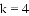



 ,则这个方程可以是______(只要求写出一个).
,则这个方程可以是______(只要求写出一个).