题目内容
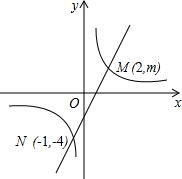 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=| k | x |
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)连接OM、ON,求三角形OMN的面积.
(3)连接OM,在x轴的正半轴上是否存在点Q,使△MOQ是等腰三角形,若存在,请直接写出所有符合条件的点Q的坐标,若不存在,说明理由.
分析:(1)把N的坐标代入反比例函数,能求出反比例函数解析式,把M的坐标代入解析式,求出M的坐标,把M、N的坐标代入y=ax+b,能求出一次函数的解析式;
(2)求出MN与x轴的交点坐标,求出△MOC和△NOC的面积即可;
(3)符合条件的有3个①OM=OQ,②OM=MQ,③MO=OQ,根据M的坐标求出即可.
(2)求出MN与x轴的交点坐标,求出△MOC和△NOC的面积即可;
(3)符合条件的有3个①OM=OQ,②OM=MQ,③MO=OQ,根据M的坐标求出即可.
解答:解:(1)把N(-1,-4)代入y=
得:k=4,
∴y=
,
把M(2,m)代入得:m=2,
∴M(2,2),
把N(-1,-4),M(2,2)代入y=ax+b得:
,
解得:a=2,b=-2,
∴y=2x-2,
答:反比例函数的解析式是y=
,一次函数的解析式是y=2x-2.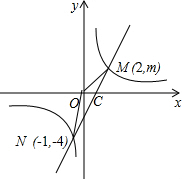
(2)设MN交x轴于C,
y=2x-2,
当y=0时,x=1,
∴C(1,0),
OC=1,
∴△MON的面积是S=S△MOC+S△NOC=
×1×2+
×1×|-4|=3,
答:三角形MON的面积是3.
(3)当OM=OQ时,Q的坐标是(2
,0);
当OM=MQ时,Q的坐标是(4,0);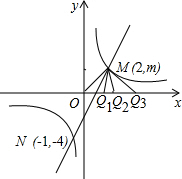
当OQ=QM时,Q的坐标是(2,0);
答:在x轴的正半轴上存在点Q,使△MOQ是等腰三角形,所有符合条件的点Q的坐标是(2
,0)或(4,0)或(2,0).
| k |
| x |
∴y=
| 4 |
| x |
把M(2,m)代入得:m=2,
∴M(2,2),
把N(-1,-4),M(2,2)代入y=ax+b得:
|
解得:a=2,b=-2,
∴y=2x-2,
答:反比例函数的解析式是y=
| 4 |
| x |
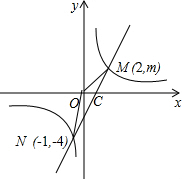
(2)设MN交x轴于C,
y=2x-2,
当y=0时,x=1,
∴C(1,0),
OC=1,
∴△MON的面积是S=S△MOC+S△NOC=
| 1 |
| 2 |
| 1 |
| 2 |
答:三角形MON的面积是3.
(3)当OM=OQ时,Q的坐标是(2
| 2 |
当OM=MQ时,Q的坐标是(4,0);
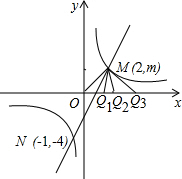
当OQ=QM时,Q的坐标是(2,0);
答:在x轴的正半轴上存在点Q,使△MOQ是等腰三角形,所有符合条件的点Q的坐标是(2
| 2 |
点评:本题综合考查了用待定系数法求一次函数和反比例函数的解析式,三角形的面积,等腰三角形的判定等知识点,此题综合性比较强,题型较好,分类讨论思想的运用.

练习册系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数