题目内容
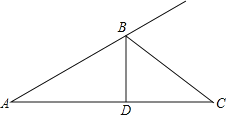
【题目】如图,在△ABC中,BD⊥AC,垂足为C,且∠A<∠C,点E是一动点,其在BC上移动,连接DE,并过点E作EF⊥DE,点F在AB的延长线上,连接DF交BC于点G.
(1)请同学们根据以上提示,在上图基础上补全示意图.
(2)当△ABD与△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠C的度数.
【答案】(1)详见解析;(2)40°.
【解析】
(1)根据垂直画出图形即可得出结论;
(2)先根据两三角形全等,判断出AB=DF,进而判断出BD=DE,再求出∠FDE=60°,进而利用三角形的外角的性质求出∠BDE=80°,进而求出∠DBE=∠BED=50°,即可得出结论.
(1)补全示意图如图所示,
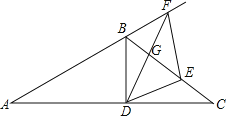
(2)∵DE⊥EF,BD⊥AC,
∴∠DEF=∠ADB=90°.
∵△ABD与△DEF全等,
∴AB=DF,
又∵AD=FE,
∴∠ABD=∠FDE,
∴BD=DE.
在Rt△ABD中,∠ABD=90°﹣∠A=60°.
∴∠FDE=60°.
∵∠ABD=∠BDF+∠AFD,
∵∠AFD=40°,
∴∠BDF=20°.
∴∠BDE=∠BDF+∠FDE=20°+60°=80°.
∵BD=DE,
∴∠DBE=∠BED=![]() (180°﹣∠BDE)=50°.
(180°﹣∠BDE)=50°.
在Rt△BDC中,∠C=90°﹣∠DBE=90°﹣50°=40°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某数学兴趣小组在本校九年级学生中以“你最喜欢的项体育运动"为主体进行了抽样调查,并将调查结果绘制成下表和下图.
项目 | 篮球 | 乒乓球 | 羽毛球 | 跳绳 | 其他 |
人数 |
| 12 | 10 | 5 | 8 |

请根据图表中的信息完成下列各题:
(1)本次共调查学生______名;
(2)![]() =______;
=______;
(3)在扇形图中,“跳绳”对应的扇形圆是______.