题目内容
如图,直线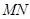 与线段
与线段 相交于点
相交于点 ,点
,点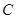 和点
和点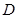 在直线
在直线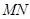 上,且
上,且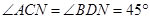 .
.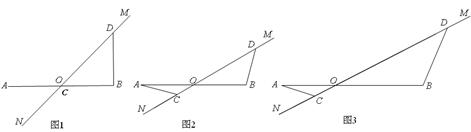
(1)如图1所示,当点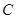 与点
与点 重合时 ,且
重合时 ,且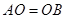 ,请写出
,请写出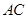 与
与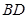 的数量关系和位置关系;
的数量关系和位置关系;
(2)将图1中的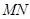 绕点
绕点 顺时针旋转到如图2所示的位置,
顺时针旋转到如图2所示的位置,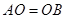 ,(1)中的
,(1)中的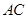 与
与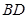 的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)将图2中的 拉长为
拉长为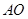 的
的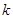 倍得到如图3,求
倍得到如图3,求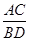 的值.
的值.
(1)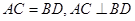 ;(3)
;(3)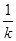
解析试题分析:(1)根据点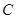 与点
与点 重合时的图形特征即可作出判断;
重合时的图形特征即可作出判断;
(2)过点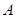 作
作 于
于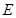 ,过点
,过点 作
作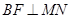 于
于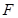 ,证得
,证得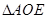 ≌
≌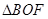 ,即得
,即得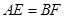 ,由
,由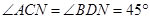 可得
可得 ,即得
,即得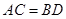 ,延长
,延长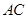 与
与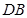 的延长线相交点
的延长线相交点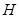 ,即得
,即得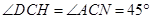 ,再结合
,再结合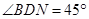 即可作出判断;
即可作出判断;
(3)过点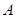 作
作 于
于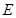 ,过点
,过点 作
作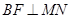 于
于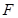 ,易证
,易证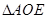 ∽
∽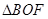 ,根据相似三角形的性质可得
,根据相似三角形的性质可得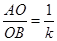 ,由(2)知
,由(2)知 ,即可求得结果.
,即可求得结果.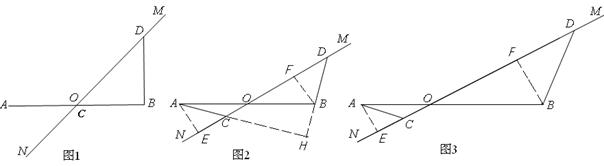
(1)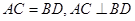 ;
;
(2)仍然成立.
过点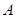 作
作 于
于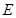 ,过点
,过点 作
作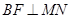 于
于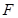
∴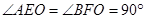
∵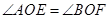 ,
,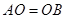
∴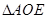 ≌
≌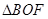
∴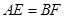
∵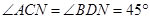
∴
∴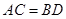
延长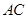 与
与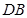 的延长线相交点
的延长线相交点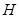
∴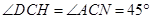
又∵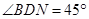
∴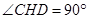
∴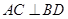 ;
;
(3)过点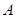 作
作 于
于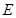 ,过点
,过点 作
作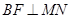 于
于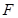
易证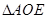 ∽
∽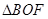
∴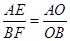
∵ ,
,
∴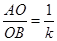 .
.
由(2)知 .
.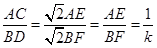 .
.
考点:旋转问题的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案(9分)如图,直线![]() 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
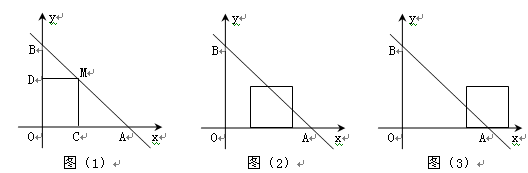 |
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为![]() ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与![]() 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.
(9分)如图,直线 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
 |
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为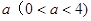 ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与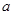 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.
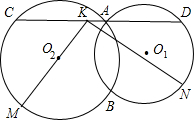 如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.
如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.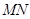 与线段
与线段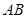 相交于点
相交于点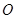 ,点
,点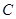 和点
和点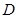 在直线
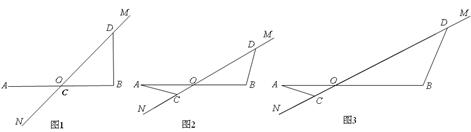
在直线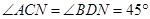 .
.
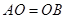 ,请写出
,请写出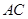 与
与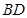 的数量关系和位置关系;
的数量关系和位置关系; 拉长为
拉长为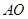 的
的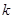 倍得到如图3,求
倍得到如图3,求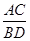 的值.
的值.