题目内容
【题目】如图1,将长为10的线段OA绕点O旋转![]() 得到OB,点A的运动轨迹为
得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
![]() 当
当![]() ______度时,PQ有最大值,最大值为______.
______度时,PQ有最大值,最大值为______.
![]() 如图2,若P是OB中点,且
如图2,若P是OB中点,且![]() 于点P,求
于点P,求![]() 的长;
的长;
![]() 如图3,将扇形AOB沿折痕AP折叠,使点B的对应点
如图3,将扇形AOB沿折痕AP折叠,使点B的对应点![]() 恰好落在OA的延长线上,求阴影部分面积.
恰好落在OA的延长线上,求阴影部分面积.
![]() 如图4,将扇形OAB沿PQ折叠,使折叠后的弧
如图4,将扇形OAB沿PQ折叠,使折叠后的弧![]() 恰好与半径OA相切,切点为C,若
恰好与半径OA相切,切点为C,若![]() ,求点O到折痕PQ的距离.
,求点O到折痕PQ的距离.




【答案】90![]()
【解析】
![]() 先判断出当PQ取最大时,点Q与点A重合,点P与点B重合,即可得出结论;
先判断出当PQ取最大时,点Q与点A重合,点P与点B重合,即可得出结论;
![]() 先判断出
先判断出![]() ,最后用弧长用弧长公式即可得出结论;
,最后用弧长用弧长公式即可得出结论;
![]() 先在
先在![]() 中,
中,![]() ,解得
,解得![]() ,最后用面积的和差即可得出结论.
,最后用面积的和差即可得出结论.
![]() 先找点O关于PQ的对称点
先找点O关于PQ的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,证明四边形
,证明四边形![]() 是矩形,由勾股定理求
是矩形,由勾股定理求![]() ,从而求出
,从而求出![]() 的长,进而得出OM.
的长,进而得出OM.
![]() 是半径OB上一动点,Q是
是半径OB上一动点,Q是![]() 上的一动点,
上的一动点,
![]() 当PQ取最大时,点Q与点A重合,点P与点B重合,
当PQ取最大时,点Q与点A重合,点P与点B重合,
此时,![]() ,
,![]() ,
,
故答案为:90,![]() ;
;
![]() 如图2,连接OQ,
如图2,连接OQ,

![]() 点P是OB的中点,
点P是OB的中点,
![]() .
.
![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ;
;
![]() 由折叠的性质可得,
由折叠的性质可得,![]() ,
,![]() ,
,
在![]() 中,
中,![]()
解得![]() ,
,
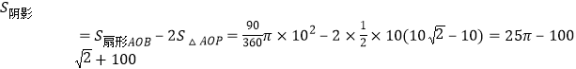 .
.
![]() 找点O关于PQ的对称点
找点O关于PQ的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,如图4,
,如图4,
则![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 所在圆的圆心,
所在圆的圆心,
![]() ,
,
![]() 折叠后的弧
折叠后的弧![]() 恰好与半径OA相切于C点,
恰好与半径OA相切于C点,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
在![]() 中,
中,![]() ,
,
在![]() ,
,![]() ,
,
![]() ,
,
即O到折痕PQ的距离为![]() ,
,

 阅读快车系列答案
阅读快车系列答案【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.





