题目内容
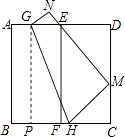
【题目】如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N 
(1)若CM=x,则CH=(用含x的代数式表示);
(2)求折痕GH的长.
【答案】
(1)﹣ ![]() x2+3
x2+3
(2)解:∵四边形ABCD为正方形,
∴∠B=∠C=∠D=90°,
设CM=x,由题意可得:ED=3,DM=6﹣x,∠EMH=∠B=90°,
故∠HMC+∠EMD=90°,
∵∠HMC+∠MHC=90°,∴∠EMD=∠MHC,
∴△EDM∽△MCH,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得:x1=2,x2=6(不合题意舍去),
∴CM=2,
∴DM=4,
∴在Rt△DEM中,由勾股定理得:EM=5,
∴NE=MN﹣EM=6﹣5=1,
∵∠NEG=∠DEM,∠N=∠D,
∴△NEG∽△DEM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:NG= ![]() ,
,
由翻折变换的性质,得AG=NG= ![]() ,
,
过点G作GP⊥BC,垂足为P,
则BP=AG= ![]() ,GP=AB=6,
,GP=AB=6,
当x=2时,CH=﹣ ![]() x2+3=
x2+3= ![]() ,
,
∴PH=BC﹣HC﹣BP=6﹣ ![]() ﹣
﹣ ![]() =2,
=2,
在Rt△GPH中,GH= ![]() =
= ![]() =2
=2 ![]() .
.
![]()
![]()

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目