题目内容
有2个信封,每个信封内各装有四张卡片,其中一个信封内的四张卡片上分别写有1、2、3、4四个数,另一个信封内的四张卡片分别写有5、6、7、8四个数,甲、乙两人商定了一个游戏,规则是:从这两个信封中各随机抽取一张卡片,然后把卡片上的两个数相乘,如果得到的积大于20,则甲获胜,否则乙获胜.
(1)请你通过列表(或画树状图)计算甲获胜的概率.
(2)你认为这个游戏公平吗?为什么?
解:(1)利用列表法得出所有可能的结果,如下表:
由上表可知,该游戏所有可能的结果共16种,其中两卡片上的数字之积大于20的有5种,所以甲获胜的概率为P甲= .
.
(2)这个游戏对双方不公平,因为甲获胜的概率P甲= ,乙获胜的概率P乙=
,乙获胜的概率P乙=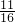 ,
,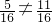 ,所以,游戏对双方是不公平的.
,所以,游戏对双方是不公平的.
分析:本题考查概率问题中的公平性问题,解决本题的关键是计算出各种情况的概率,然后比较即可.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
| 1 | 2 | 3 | 4 | |
| 5 | 5 | 10 | 15 | 20 |
| 6 | 6 | 12 | 18 | 24 |
| 7 | 7 | 14 | 21 | 28 |
| 8 | 8 | 16 | 24 | 32 |
 .
.(2)这个游戏对双方不公平,因为甲获胜的概率P甲=
 ,乙获胜的概率P乙=
,乙获胜的概率P乙=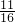 ,
,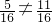 ,所以,游戏对双方是不公平的.
,所以,游戏对双方是不公平的.分析:本题考查概率问题中的公平性问题,解决本题的关键是计算出各种情况的概率,然后比较即可.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目