题目内容
(本小题满分15分)如图1,抛物线![]() 经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2.
经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2.
(1)求![]() 的值及点B的坐标;
的值及点B的坐标;
(2)设点D为线段AB上的一个动点,过D作x轴的垂线,垂足为点H.在DH的右侧作等边△DHG. 将过抛物线顶点M的直线记为![]() ,设
,设![]() 与x轴交于点N.
与x轴交于点N.
① 如图1,当动点D的坐标为(1,2)时,若直线![]() 过△DHG的顶点G.求此时点N的横坐标是多少?
过△DHG的顶点G.求此时点N的横坐标是多少?
② 若直线![]() 与△DHG的边DG相交,试求点N横坐标的取值范围.
与△DHG的边DG相交,试求点N横坐标的取值范围.
(1)∵ 点A(2,4)在抛物线![]() 上,
上,
∴代入得 ![]() =1 ……………………………1分
=1 ……………………………1分
于是抛物线的解析式为![]()
又∵点B的横坐标为-2,代入得![]() ∴ B(-2,-4) ………………2分
∴ B(-2,-4) ………………2分
(2)①由题意 M(1,5),D(1,2),且DH⊥x轴,
∴ 点M在DH上,MH=5.
过点G作GE⊥DH,垂足为E.
∵△DHG是正三角形,可得EG=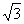 , EH=1,
, EH=1,
∴ ME=4.
设N ( x,0 ),则 NH=x-1,
由△MEG∽△MHN,得![]() . ………………5分
. ………………5分
∴![]() , 解得
, 解得 ![]()
![]()
∴点N的横坐标为![]() . ……………………6分
. ……………………6分
 ②如右图,当点D运动至与点A重合时,直线
②如右图,当点D运动至与点A重合时,直线![]() 与DG交于点G,此时点N的横坐标最大.
与DG交于点G,此时点N的横坐标最大.
过点G,M作x轴的垂线,垂足分别为点Q,F.设N(x,0)
∵ A (2, 4), ∴ G (![]() , 2)
, 2)
∴ NQ=![]() ,NF =
,NF = ,GQ=2,MF =5.
,GQ=2,MF =5.
由题意,
△NGQ∽△NMF,
∴![]() . ……………………9分
. ……………………9分
∴![]() .
.
∴![]() . ……………………10分
. ……………………10分
 如右图,当点D运动至与点B重合时,直线
如右图,当点D运动至与点B重合时,直线![]() 与DG交于点D(即点B)此时点N的横坐标最小. ∵B(-2, -4) ,∴ H(-2, 0),D(-2, -4).设N(x,0).由题意△BHN∽△MFN,
与DG交于点D(即点B)此时点N的横坐标最小. ∵B(-2, -4) ,∴ H(-2, 0),D(-2, -4).设N(x,0).由题意△BHN∽△MFN,
∴![]() . ……………………13分
. ……………………13分
∴ ![]() ∴
∴ ![]() ……………………14分
……………………14分
综上,点N的横坐标取值范围是![]() ≤x≤
≤x≤![]() ……15分
……15分
解析:略

 同步练习强化拓展系列答案
同步练习强化拓展系列答案
 在点(1,-2)处的切线方程;
在点(1,-2)处的切线方程;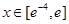 上的图象与直线
上的图象与直线 总有两个不同交点,求实数a的取值范围。
总有两个不同交点,求实数a的取值范围。
 在点(1,-2)处的切线方程;
在点(1,-2)处的切线方程;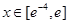 上的图象与直线
上的图象与直线 总有两个不同交点,求实数a的取值范围。
总有两个不同交点,求实数a的取值范围。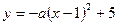 经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2.
经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2.
 的值及点B的坐标;
的值及点B的坐标;  ,设
,设 过△DHG的顶点G.求此时点N的横坐标是多少?
过△DHG的顶点G.求此时点N的横坐标是多少? 经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2.
经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2. 的值及点B的坐标;
的值及点B的坐标;  ,设
,设 过△DHG的顶点G.求此时点N的横坐标是多少?
过△DHG的顶点G.求此时点N的横坐标是多少?