题目内容
如图，直线y=a分别与双曲线
和直线y=
x交于A，D两点，过点A，点D分别作x轴的垂线段，垂足为点B，C，若四边形ABCD是正方形，则a的值为________．
1
分析：根据双曲线与直线解析式求出点A、D的坐标，然后求出AD、AB的长度，再根据正方形的邻边相等列出方程求解即可．
解答：∵y=a与y=
交于点A，
∴=a，
解得x=
，
∴点A（，a），
∵y=a与y=x相交于点D，
∴x=a，
解得x=2a，
∴点D（2a，a），
∴AB=a，AD=2a-，
∵四边形ABCD是正方形，
∴AB=AD，
∴2a-=a，
解得a1=1，a2=-1（舍去），
故答案为：1．
点评：本题考查了反比例函数与一次函数的交点问题，正方形的邻边相等的性质，根据函数解析式求出点A、D的坐标是解题的关键．
分析：根据双曲线与直线解析式求出点A、D的坐标，然后求出AD、AB的长度，再根据正方形的邻边相等列出方程求解即可．
解答：∵y=a与y=
交于点A，∴
=a，解得x=
，∴点A（
，a），∵y=a与y=
x相交于点D，∴
x=a，解得x=2a，
∴点D（2a，a），
∴AB=a，AD=2a-
，∵四边形ABCD是正方形，
∴AB=AD，
∴2a-
=a，解得a1=1，a2=-1（舍去），
故答案为：1．
点评：本题考查了反比例函数与一次函数的交点问题，正方形的邻边相等的性质，根据函数解析式求出点A、D的坐标是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知：如图，直线y=-x+4分别与x轴，y轴交于A、B两点，从点P（2，0）射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是（ ）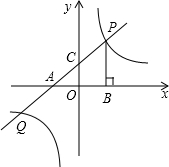
曲线
（2012•青浦区二模）如图，直线y=x+1分别与 x轴、y轴分别相交于点A、B．抛物线y=ax2+bx+c（a≠0）与 y轴的正半轴相交于点C，与这个一次函数的图象相交于A、D，且sin∠ACB=
如图，直线y=a分别与双曲线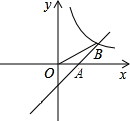
如图，直线y=x-1分别交x轴、反比例函数y=