题目内容
已知,如图,直线分别交x轴、y轴于点A(-4,0),C,点P(2,m)是直线AC与双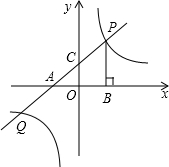 曲线y=
曲线y=| k | x |
(1)求m值;
(2)求两个函数的解析式;
(3)在第一象限内x为何值时一次函数大于反比例函数?
分析:(1)由图可知AB=6,又△APB的面积为6,所以可求m值;
(2)因为点P(2,2)在双曲线y=
上,所以K=2×2=4,可求反比例函数解析式;直线经过点A(-4,0)、点P(2,2),运用代入法易求一次函数解析式;
(3)同一范围内图象位置高者,函数值大,因此当x>2时,在第一象限内一次函数大于反比例函数.
(2)因为点P(2,2)在双曲线y=
| k |
| x |
(3)同一范围内图象位置高者,函数值大,因此当x>2时,在第一象限内一次函数大于反比例函数.
解答:解:(1)∵AB=4+2=6
AB×PB=6
∴PB=2
∴m=2(2分)
(2)∵S△ABP=
×AB×BP
∴6=
×6×BP
∴BP=2
∴P(2,2)
设y=kx+b 0=-4k+b 2=2k+b
解得:k=
,b=
(6分)
∴y=
x+
∵点P(2,2)在双曲线y=
上
∴K=2×2=4
∴Y=
.
(3)当x>2时,在第一象限内一次函数大于反比例函数.(8分)
| 1 |
| 2 |
∴PB=2
∴m=2(2分)
(2)∵S△ABP=
| 1 |
| 2 |
∴6=
| 1 |
| 2 |
∴BP=2
∴P(2,2)
设y=kx+b 0=-4k+b 2=2k+b
解得:k=
| 1 |
| 3 |
| 4 |
| 3 |
∴y=
| 1 |
| 3 |
| 4 |
| 3 |
∵点P(2,2)在双曲线y=
| k |
| x |
∴K=2×2=4
∴Y=
| 4 |
| x |
(3)当x>2时,在第一象限内一次函数大于反比例函数.(8分)
点评:此题难度中等,考查反比例函数、一次函数的图象和性质及运用待定系数法求解析式.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( ) 分别交
分别交 ,
, 于点
于点 ,
, ,且∠AEF=
,且∠AEF= ,
, 的平分线与
的平分线与 的平分线相交于点
的平分线相交于点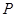 .
.
 ,求
,求 的度数.
的度数. 分别交
分别交 ,
, 于点
于点 ,
, ,且∠AEF=
,且∠AEF=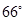 ,
, 的平分线与
的平分线与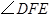 的平分线相交于点
的平分线相交于点 .
.
 ,求
,求 的度数.
的度数. 分别与
分别与 轴,
轴, 轴交于
轴交于 两点,从点
两点,从点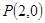 射出的光线经直线
射出的光线经直线 反射后再射到直线
反射后再射到直线 上,最后经直线
上,最后经直线 点,则光线所经过的路程是( )
点,则光线所经过的路程是( ) B.
B.
 C.
C. D.
D. 
