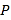题目内容
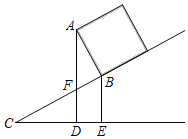
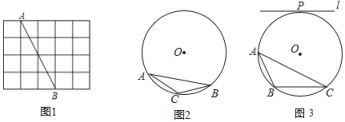
【题目】(1)如图1,网格中每个小正方形的边长为1,点A,B均在格点上.则线段AB的长为 .请借助网格,仅用无刻度的直尺在AB上作出点P,使AP=![]() .
.
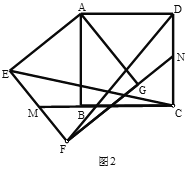
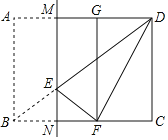
(2)⊙O为△ABC的外接圆,请仅用无刻度的直尺,依下列条件分别在图2,图3的圆中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法,请下结论注明你所画的弦).
①如图2,AC=BC;
②如图3,P为圆上一点,直线l⊥OP且l∥BC.
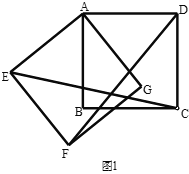
【答案】(1)2![]() ,画图作出点P见解析;(2)①画图见解析,② 画图见解析.
,画图作出点P见解析;(2)①画图见解析,② 画图见解析.
【解析】
(1)利用勾股定理列式求出AB=2![]() ,然后利用相似三角形的判定与性质构造相似三角形,满足AP:BP=2:1即可;
,然后利用相似三角形的判定与性质构造相似三角形,满足AP:BP=2:1即可;
(2)①过点C作直径CD,由于AC=BC,弧AC=弧BC,根据垂径定理的推理得CD垂直平分AB,所以CD将△ABC分成面积相等的两部分;
②连结PO并延长交BC于E,过点A、E作弦AD,由于直线l与⊙O相切于点P,根据切线的性质得OP⊥l,而l∥BC,则PE⊥BC,根据垂径定理得BE=CE,所以弦AE将△ABC分成面积相等的两部分.
(1)AB=![]() 2
2![]() ,作图如图所示;所以,AP=
,作图如图所示;所以,AP=![]() 时AP:BP=2:1.
时AP:BP=2:1.
点P如图所示.取格点M,N,连接MN交AB于P,则点P即为所求;

(2)①如图1,CD即为所求;

②如图2,CD即为所求.

练习册系列答案
相关题目