题目内容
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形,例如△ABC中,三边分别为a、b、c,若满足b2=ac,则称△ABC为比例三角形,其中b为比例中项.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
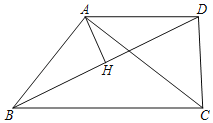
(2)如图,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.
①请直接写出图中的比例三角形;
②作AH⊥BD,当∠ADC=90°时,求![]() 的值;
的值;
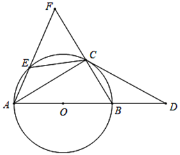
(3)三边长分别为a、b、c的三角形是比例三角形,且b为比例中项,已知抛物线y=ax2+bx+c与y轴交于点B,顶点为A,O为坐标原点,以OB为直径的⊙M经过点A,记△OAB的面积为S1,⊙M的面积为S2,试问S1:S2的值是否为定值?若是请求出定值,若不是请求出S1:S2的取值范围.
【答案】(1)AC=![]() ;
;
(2)①△ADC是比例三角形;②![]() ;
;
(3)![]() =
=![]() .
.
【解析】
(1)分三种情况讨论,由比例三角形的定义可求解;
(2)①通过证明△ABC∽△DCA,可得![]() ,可得AD2=ACCD,可得△ADC是比例三角形;
,可得AD2=ACCD,可得△ADC是比例三角形;
②由勾股定理可得AB2+AC2=BC2,AD2+CD2=AC2,BC2+CD2=BD2,可得BD=![]() AC,即可求解;
AC,即可求解;
(3)分别求出S1,S2,由勾股定理可求b的值,即可求解.
解:(1)∵△ABC是比例三角形,AB=2,BC=3,
∴若AB是比例中项,则AB2=BC×AC,
∴AC=![]() ,
,
若AC是比例中项,则AC2=BC×AB,
∴AC=![]() ,
,
若BC是比例中项,则BC2=AC×AB,
∴AC=![]()
(2)①△ADC是比例三角形,
理由如下,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AD∥BC,
∴∠ACB=∠DAC,∠ADB=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∵∠DAC=∠ACB,∠BAC=∠ADC,
∴△ABC∽△DCA,
∴![]() ,且AD=AB,
,且AD=AB,
∴AD2=ACCD,
∴△ADC是比例三角形;
②∵∠ADC=90°=∠BAC,AD∥BC,
∴∠ADC=∠BCD=90°,
∵AB2+AC2=BC2,AD2+CD2=AC2,BC2+CD2=BD2,
∴2AC2=BD2,
∴BD=![]() AC,
AC,
∵AB=AD,AH⊥BD,
∴BH=![]() BD=
BD=![]() AC,
AC,
∴![]()
(3)∵三边长分别为a、b、c的三角形是比例三角形,且b为比例中项,
∴b2=ac,a>0,b>0,c>0,
∵已知抛物线y=ax2+bx+c与y轴交于点B,顶点为A,
∴B(0,c),点A(﹣![]() ,
,![]() )
)
∴点A(﹣![]() ,
,![]() c)
c)
∵S1=![]() ×c×
×c×![]() =
=![]() ,
,
S2=π×(![]() c)2=
c)2=![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∵以OB为直径的⊙M经过点A,
∴∠OAB=90°,
∴OA2+OB2=OC2,
∴(![]() )2+(
)2+(![]() c)2+(
c)2+(![]() )2+(c﹣
)2+(c﹣![]() c)2=c2,
c)2=c2,
∴![]() a2c2=b2,
a2c2=b2,
∴(![]() b2﹣1)b2=0,
b2﹣1)b2=0,
∴b=![]() ,
,
∴![]() =
=![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案