��Ŀ����
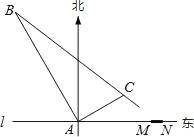
����Ŀ���ڶ�������ĺ�����l����һ��Ϊ1km����ͷMN����ͼ��������ͷ����M������19.5km����һ�۲�վA��ijʱ�̲��һ������ֱ�ߺ��е��ִ�λ��A�ı�ƫ��30��������A���40km��B��������1Сʱ20���ӣ��ֲ�ø��ִ�λ��A�ı�ƫ��60��������A���![]() km��C����
km��C����
��1������ִ����е��ٶȣ�������ȷ�������
��2��������ִ����ı亽��������У���ô�ִ��ܷ�����������ͷMN��������˵�����ɣ�
���𰸡���1��12![]() ��ǧ��/Сʱ������2�����ִ��ܹ�����������ͷMN������
��ǧ��/Сʱ������2�����ִ��ܹ�����������ͷMN������
�������������������1�����ݡ�1=30�㣬��2=60������֪��ABCΪֱ�������Σ����ݹ��ɶ������
��2���ӳ�BC��l��T���Ƚ�AT��AM��AN�Ĵ�С���ɵó����ۣ�
�����������1���ߡ�1=30�㣬��2=60�㣬
���ABCΪֱ�������Σ�
��AB=40km��AC=![]() km��
km��
��BC=![]() ��km����
��km����
��1Сʱ20����=80���ӣ�1Сʱ=60���ӣ�
��![]() ��60=12
��60=12![]() ��ǧ��/Сʱ����
��ǧ��/Сʱ����
��2���ܣ�
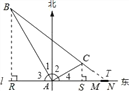
���ɣ����߶�BR��AN��R�����߶�CS��AN��S���ӳ�BC��l��T��
�ߡ�2=60�㣬
���4=90�㩁60��=30�㣮
��AC=8![]() ��km����
��km����
��CS=8![]() sin30��=4
sin30��=4![]() ��km����
��km����
��AS=8![]() cos30��=8
cos30��=8![]() ��
��![]() =12��km����
=12��km����
�֡ߡ�1=30�㣬
���3=90�㩁30��=60�㣮
��AB=40km��
��BR=40sin60��=20![]() ��km����
��km����
��AR=40��cos60��=40��![]() =20��km����
=20��km����
�ã���STC�ס�RTB��
����![]() ��
��
![]() .
.
��ã�ST=8��km����
����AT=12+8=20��km����
����ΪAM=19.5km��MN��Ϊ1km����AN=20.5km��
��19.5��AT��20.5
���ִ��ܹ�����������ͷMN������

 ��У����ϵ�д�
��У����ϵ�д�