Question

【题目】对于任意正实数a、b，因为≥0，所以a﹣≥0，所以a+b≥，只有当a=b时，等号成立．

【获得结论】在a+b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a=b时，a+b有最小值2．

根据上述内容，回答下列问题：若m＞0，只有当m= 时，m+有最小值 ．

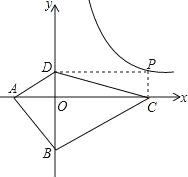
【探索应用】如图，已知A（﹣3，0），B（0，﹣4），P为双曲线上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

Answer 1

【答案】（1）1，2；（2)见试题解析。

【解析】

试题分析：（1）根据题目所给信息可知m+≥2，且当m=时等号成立，可得出答案；

（2）可设P（x，），可表示出AC和BD，则四边形ABCD的面积为S四边形ABCD=2（x+）+12，再利用所给信息可得到其最小值，此时x=3，可得出AC=BD，可得出四边形ABCD为菱形．

试题解析：（1）根据题目所给信息可知m+≥2，且当m=时等号，

∴当m=1时，m+≥2，即当m=1时，m+有最小值2，

故答案为：1，2；

（2）设P（x，），则C（x，0），D（0，），

∴CA=x+3，BD=+4，

∴S四边形ABCD=CA×BD=（x+3）（+4），

化简得：S=2（x+）+12，∵x＞0，＞0，∴x+≥2=6，

只有当x=，即x=3时，等号成立，∴S≥2×6+12=24．

∴S四边形ABCD有最小值24，此时，P（3，4），C（3，0），D（0，4），

AB=BC=CD=DA=5，∴四边形ABCD是菱形．