��Ŀ����
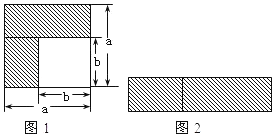
����Ŀ����ͼ1�����ֱ��ԡ�ABC��AC��BC����Ϊ������������ı���ACDE��BCFGΪ�����Σ����������������Ϊ��չ˫Ҷ�����Σ�
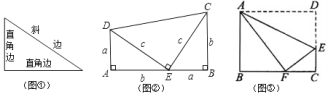
��1�����֣���ͼ2������C=90��ʱ����֤����ABC���DCF�������ȣ�
��2�����꣺�����C![]() 90��ʱ����1���н��ۻ�������������������ͼ1����֤����������������˵�����ɣ�
90��ʱ����1���н��ۻ�������������������ͼ1����֤����������������˵�����ɣ�
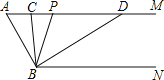
��3�����ã���ͼ3���ֱ��ԡ�ABC������Ϊ������������ı���ACDE��BCFG��ABMNΪ�����Σ����������������Ϊ��չ��Ҷ�����Σ���֪��ABC�У�AC=3��BC=4������C=_____��ʱ��ͼ����Ӱ���ֵ�����������ֵ��________��

���𰸡���1��֤������������2��������֤������������3��18.
��������
���⣨1����ΪAC=DC����ACB=��DCF=90����BC=FC��������ABC�ա�DFC���Ӷ���ABC����DFC�������ȣ�
��2���ӳ�BC����P������A��AP��BP�ڵ�P������D��DQ��FC�ڵ�Q���õ��ı���ACDE��BCFG��Ϊ�����Σ�AC=CD��BC=CF����ACP=��DCQ��������APC�ա�DQC��
����AP=DQ������ΪS��ABC=![]() BCAP��S��DFC=
BCAP��S��DFC=![]() FCDQ������S��ABC=S��DFC��
FCDQ������S��ABC=S��DFC��
��3�����ݣ�2����ͼ����Ӱ���ֵ����������ABC�������������ͼ����Ӱ���ֵ�����������ֵ����������ABC����������ABC��ֱ�������Σ�����C��90��ʱ����Ӱ���ֵ�������������S��Ӱ���������=3S��ABC=3��![]() ��3��4=18��
��3��4=18��
��1��֤��������ABC����DFC�У�
��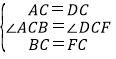 ��
��
���ABC�ա�DFC��
���ABC����DFC�������ȣ�
��2���⣺�������������£�
��ͼ���ӳ�BC����P������A��AP��BP�ڵ�P������D��DQ��FC�ڵ�Q��
���APC=��DQC=90����
���ı���ACDE��BCFG��Ϊ�����Σ�
��AC=CD��BC=CF����ACP+��PCD=90������DCQ+��PCD=90����
���ACP=��DCQ��
��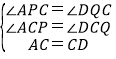 ��
��
��APC�ա�DQC��AAS����
��AP=DQ��
����S��ABC=![]() BCAP��S��DFC=
BCAP��S��DFC=![]() FCDQ��
FCDQ��
��S��ABC=S��DFC��
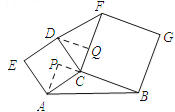
��3���⣺���ݣ�2����ͼ����Ӱ���ֵ����������ABC�����������
��ͼ����Ӱ���ֵ�����������ֵ����������ABC��������
������ABC��ֱ�������Σ�����C��90��ʱ����Ӱ���ֵ���������
��S��Ӱ���������=3S��ABC=3��![]() ��3��4=18��
��3��4=18��

����Ŀ���ٻ����л��������ƺŵ�![]() ����ȹ����������Ⱥ����ޣ�����֭55%���ϣ����ܹ�����Ի�����ϲ��������20��
����ȹ����������Ⱥ����ޣ�����֭55%���ϣ����ܹ�����Ի�����ϲ��������20��![]() ����ȣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ,��¼���£�
����ȣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ,��¼���£�
��������IJ�ֵ ����λ��ǧ�ˣ� | -3 | -2 | -1��5 | 0 | 1 | 2��5 |
���� | 1 | 4 | 2 | 3 | 2 | 8 |
��1������20��![]() �������,���ص�һ��������һ���ض���ǧ�ˣ�
�������,���ص�һ��������һ���ض���ǧ�ˣ�
��2����������Ƚϣ�20��![]() ������ܼƳ����������ǧ�ˣ�
������ܼƳ����������ǧ�ˣ�
��3����![]() �����ÿǧ���ۼ�8Ԫ������20��
�����ÿǧ���ۼ�8Ԫ������20��![]() ����ȿ�������Ԫ��
����ȿ�������Ԫ��