Question

【题目】探索发现:

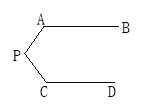
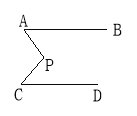
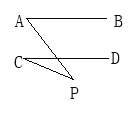
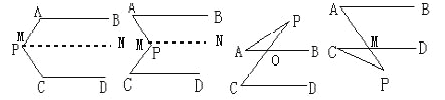
如图所示,已知AB∥CD,分别写出下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选二个加以说明.

Answer 1

【答案】证明见解析.

【解析】

试题分析：（1），（2）都需要用到辅助线利用两直线平行，内错角相等的定理加以证明；

（3），（4）是利用两直线平行，同位角相等的定理和三角形外角的性质加以证明．

试题解析：（1）∠A+∠C+∠P=360；

（2）∠A+∠C=∠P；

（3）∠A+∠P=∠C；

（4）∠C+∠P=∠A.

说明理由：(1)过点P作AB的平行线,MN∥AB.

∵MN∥AB,

∴∠A+∠APM=180°

又∵MN∥CD,

∴∠C+∠CPM=180°

∴∠A+∠C＋∠APM＋∠OPM=∠A+∠C+∠P=360°.

(2)过P作MN∥AB,

∵MN∥AB,

∴∠A=∠APM,

∵MN∥CD,

∴∠C=∠CPM,

∴∠A+∠C=∠APM+∠CPM=∠P.

(3)令AB,CP交点为O,

∵AB∥CD,

∴∠C=∠POB,

又∵∠A+∠P+∠POA=180°, ∠POB+∠POA=180°,

∴∠A+∠P=∠POB=∠C.

(4)令AP,CD交点为M,

∵AB∥CD,

∴∠A=∠PMD,

∵∠C+∠P+∠CMP=180°, ∠PMD+∠PMC=180°,

∴∠C+∠P=∠PMD=∠A.