Question

【题目】如图，在Rt△ABC中，∠ABC=90°，点M是AC的中点，以AB为直径作⊙O分别交AC，BM于点D，E．连结DE，使四边形DEBA为⊙O的内接四边形．

（1）求证：∠A=∠ABM=∠MDE；

（2）若AB=6，当AD=2DM时，求DE的长度；

（3）连接OD，OE，当∠A的度数为60°时，求证：四边形ODME是菱形．

Answer 1

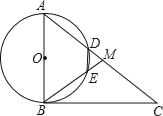
【答案】（1）证明见解析；（2）2；（3）证明见解析

【解析】试题分析：

（1）由∠ABC=90°及M是AC的中点可得AM=CM=BM，从而可得∠A=∠ABM，由四边形DEBA为⊙O的内接四边形可得∠ABM=∠MDE，由此即可得到∠A=∠ABM=∠MDE；

（2） 由（1）中结论可得DE∥AB，由此可得∴△MDE∽△MAB，从而可得结合AD=2DM及AB=6即可解得DE=2；

（3）如下图，由（1）中结论和∠A=60°易得∠AMB=60°，结合OA=OD=OE=OB可得△AOD、△OBE都是等边三角形，由此可得∠ADO=∠AMB=∠OEB=60°，由此可得OD∥BM，AM∥OE，这样即可得到四边形ODME是平行四边形，再结合OD=OE即可得到四边形ODME是菱形.

试题解析：

（1）∵∠ABC=90°，点M是AC的中点，

∴AM=CM=BM．

∴∠A=∠ABM．

∵四边形DEBA为⊙O的内接四边形，

∴∠ABM=∠MDE，

∴∠A=∠ABM=∠MDE．

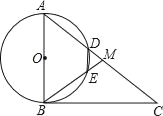
（2）由（1）知∠A=∠ABM=∠MDE，

∴DE∥AB

∴△MDE∽△MAB

∴，

∵AD=2DM，

∴AM=3DM

∴，

∴DE=2．

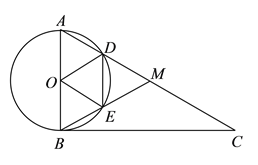
（3）由（1）知∠A=∠ABM=∠MDE，

∵∠A=60°，

∴∠A=∠ABM=∠MDE=60°

∴∠AMB=60°

又∵OA=OD=OE=OB

∴△AOD、△OBE都是等边三角形

∴∠ADO=∠AMB=∠OEB=60°，

∴OD∥BM，AM∥OE

∴四边形ODME是平行四边形，

又∵OD=OE

∴四边形ODME是菱形