��Ŀ����
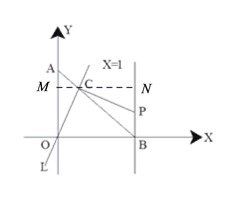
����Ŀ����ͼ����A��y���ϣ���B��x���ϣ���OA=OB=1������ԭ��O��ֱ��![]() ���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��
���߶�AB�ڵ�C����C��OC�Ĵ��ߣ���ֱ��x=1�ཻ�ڵ�P���ֽ�ֱ��![]() ��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����
��O����ת��ʹ����C��A��B�˶�����C������ڵ�һ�����ڣ�����AC�ij�Ϊt��������ͼ��������������̽����
��1������AOC����BCPȫ��ʱ�����t��ֵ��
��2��ͨ�����ֲ����߶�OC��CP�ij����ж�����֮��Ĵ�С��ϵ����֤����õ��Ľ��ۡ�
��3�������P������Ϊ��1,b��,��д��b����t�ĺ�����ϵʽ�ͱ���t��ȡֵ��Χ�����������PBCΪ����������ʱ��P�����ꡣ
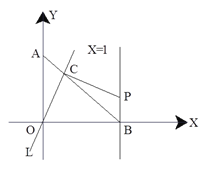
���𰸡�(1) t=![]() ��(2)��������(3) P��1.1��, P��1��1��
��(2)��������(3) P��1.1��, P��1��1��![]() ��
��
��������������
��1������֪������OA=OB=1��AB=![]() ������AOC����BCPȫ�ȿɵ�BC=OA=1���Ӷ��ɵ�t=AC=AB-BC=
������AOC����BCPȫ�ȿɵ�BC=OA=1���Ӷ��ɵ�t=AC=AB-BC=![]() ��
��
��2������C��x���ƽ���߽�OA�ڵ�M����PB�ڵ�N����������OM=BN=CN����OMC=��CNP=90�㣬��COM=��PCN���ɴ˿ɵá�OMC�ա�CNP���Ӷ��ɵ�OC=PC��
��3�����ɡ�OMC�ա�CNP���ɵ�PN=MC=AM�����AM=sin45��![]() AC=
AC=![]() ���ɴ˿ɵ�BN=OM=1-AM=
���ɴ˿ɵ�BN=OM=1-AM=![]() ���Ӷ��ɵ�PB=b=BN-PN=
���Ӷ��ɵ�PB=b=BN-PN=![]() ����b=
����b=![]() ���ɵ�C�ڵ�һ���ɵ�t��ȡֵ��Χ�ǣ�
���ɵ�C�ڵ�һ���ɵ�t��ȡֵ��Χ�ǣ�![]() �������ݵ�Cֻ���ڵ�һ���ޣ���������PC=PB��PB=BC����������ۼ��㼴��.
�������ݵ�Cֻ���ڵ�һ���ޣ���������PC=PB��PB=BC����������ۼ��㼴��.
��⣺
��1����OA=OB=1����AOB=90�㣬
��AB=![]() ��
��
�ߡ�AOC����BCPȫ����
��BC=OA=1��
��AC=AB-BC=![]() ����
����![]() ��
��
��2������C��x���ƽ���߽�OA�ڵ�M����PB�ڵ�N��
���CMO=��OCP=��CNB=90�㣬
���ı���OBNM�Ǿ��Σ���MOC+��MCO=90�㣬��MCO+��NCP=90�㣬
��BN=OM����MOC=��NCP��
��OA=OB=1,
���BAO=��ABO=��ABN=45�㣬
���BCN�ǵ���ֱ����������
��OM=BN=CN��
���MOC�ա�NCP��
��OC=PC��
��3���� ��OA=OB=1,��AOB=90�㣬
���BAO=��ABO=45�㣬
���ߡ�AMC=90�㣬
��AM=MC=AC��sin45��=![]() ��
��
��OM=OA-AM=![]() ��
��
������2����֪��BN=OM��
��NB=![]() ,
,
�ߡ�AOC����BCPȫ����
��PN=CM=AM=![]() ��
��
��PB=BN-PN=![]() ����b=
����b=![]() ��
��
����C�ڵ�һ���ޣ�
��![]() ��
��
����t=0ʱ����PBC�ǵ���ֱ�������Σ�����ʱ��C���A�غϣ����ڵ�һ���ޣ�����������Ҫ�ʴ��������������
��PB=BCʱ���ɣ�2����֪![]() �����t=1��t=-1����ȥ����
�����t=1��t=-1����ȥ����
����t=1ʱ����PBC�ǵ��������Σ���ʱ��P������Ϊ![]() ��
��
��������������PBCΪ����������ʱ����P������Ϊ![]() .
.

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�