题目内容
有一张矩形纸片ABCD,AB=5,AD=3,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则CF的长为________.

2
分析:由矩形的性质可知,AD=BC,由折叠可知DE=BC,故AD=DE,∠DEA=45°,可得∠FEC=45°,可知FC=CE=DB=AB-AD.
解答:由折叠的性质可知∠EAD= ∠DAB=45°,∠ADE=90°,
∠DAB=45°,∠ADE=90°,
∴∠DEA=45°,∠FEC=45°,
∴FC=CE=DB=AB-AD=5-3=2.
故本题答案为:2.
点评:本题考查了折叠的性质.折叠前后对应角相等,对应线段相等,关键是推出特殊三角形.
分析:由矩形的性质可知,AD=BC,由折叠可知DE=BC,故AD=DE,∠DEA=45°,可得∠FEC=45°,可知FC=CE=DB=AB-AD.
解答:由折叠的性质可知∠EAD=
 ∠DAB=45°,∠ADE=90°,
∠DAB=45°,∠ADE=90°,∴∠DEA=45°,∠FEC=45°,
∴FC=CE=DB=AB-AD=5-3=2.
故本题答案为:2.
点评:本题考查了折叠的性质.折叠前后对应角相等,对应线段相等,关键是推出特殊三角形.

练习册系列答案
相关题目
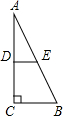 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
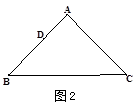



 = ;
= ; 
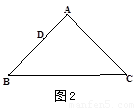
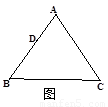
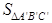 = ;
= ; 