Question

【题目】（8分）已知二次函数的图象与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，顶点为D．

（1）求以A，B，C，D为顶点的四边形的面积；

（2）在抛物线上是否存在点P，使得△ABP的面积是△ABC的面积的2倍？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）18；（2）P1（，10），P2（，10）．

【解析】试题分析：（1）分别求出二次函数与坐标轴交点坐标，D点坐标，求面积.

(2)假设存在点P，△ABP的面积是△ABC同底，△ABP高为P点纵坐标，可求得P点坐标.

解：（1）令y=0， ，解得 .

∴点A（1，0），B（5，0）.

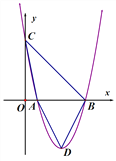
令x=0，得y=5，∴点C（0，5）,

∵，

∴点D（3，-4）,

∴以A，B，C，D为顶点的四边形的面积为

.

（2）△ABP的面积是△ABC的面积的2倍，且两个三角形底边相同，

∴，∵，∴，

解得点P1（，10），P2（，10）．