题目内容
两个相似三角形周长的比是2:3,它们的面积差是25,则较大的三角形的面积是
- A.75
- B.65
- C.50
- D.45
D
分析:由两个相似三角形周长的比是2:3,根据相似三角形周长的比等于相似比,即可得它们的相似比是2:3,又由相似三角形面积的比等于相似比的平方,求得它们的面积为4:9,由它们的面积差是25,即可求得答案.
解答:∵两个相似三角形周长的比是2:3,
∴它们的相似比是2:3,
∴它们的面积比是4:9,
设它们的面积分别为:4x,9x,
∵它们的面积差是25,
∴9x-4x=25,
解得:x=5,
∴较大的三角形的面积是:9x=45.
故选D.
点评:此题考查了相似三角形的性质.此题比较简单,注意相似三角形周长的比等于相似比与相似三角形面积的比等于相似比的平方定理的应用.
分析:由两个相似三角形周长的比是2:3,根据相似三角形周长的比等于相似比,即可得它们的相似比是2:3,又由相似三角形面积的比等于相似比的平方,求得它们的面积为4:9,由它们的面积差是25,即可求得答案.
解答:∵两个相似三角形周长的比是2:3,
∴它们的相似比是2:3,
∴它们的面积比是4:9,
设它们的面积分别为:4x,9x,
∵它们的面积差是25,
∴9x-4x=25,
解得:x=5,
∴较大的三角形的面积是:9x=45.
故选D.
点评:此题考查了相似三角形的性质.此题比较简单,注意相似三角形周长的比等于相似比与相似三角形面积的比等于相似比的平方定理的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
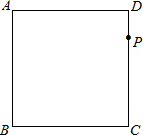 如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与P重合,并且一条直角边经过点B,另一条直角边所在的直线交于点E.
如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与P重合,并且一条直角边经过点B,另一条直角边所在的直线交于点E.