题目内容
【题目】![]() 网络比
网络比![]() 网络的传输速度快10倍以上,因此人们对
网络的传输速度快10倍以上,因此人们对![]() 产品充满期待.华为集团计划2020年元月开始销售一款
产品充满期待.华为集团计划2020年元月开始销售一款![]() 产品.根据市场营销部的规划,该产品的销售价格将随销售月份的变化而变化.若该产品第
产品.根据市场营销部的规划,该产品的销售价格将随销售月份的变化而变化.若该产品第![]() 个月(
个月(![]() 为正整数)销售价格为
为正整数)销售价格为![]() 元/台,
元/台,![]() 与
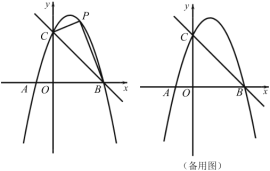
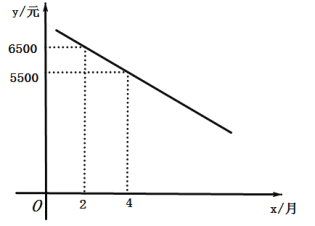
与![]() 满足如图所示的一次函数关系:且第
满足如图所示的一次函数关系:且第![]() 个月的销售数量
个月的销售数量![]() (万台)与
(万台)与![]() 的关系为
的关系为![]() .
.
(1)该产品第6个月每台销售价格为______元;
(2)求该产品第几个月的销售额最大?该月的销售价格是多少元/台?
(3)若华为董事会要求销售该产品的月销售额不低于27500万元,则预计销售部符合销售要求的是哪几个月?
(4)若每销售1万台该产品需要在销售额中扣除![]() 元推广费用,当
元推广费用,当![]() 时销售利润最大值为22500万元时,求
时销售利润最大值为22500万元时,求![]() 的值.
的值.
【答案】(1)4500元;(2)7,4000;(3)4、5、6、7、8、9、10;(4)![]() .
.
【解析】
(1)利用待定系数法将(2,6500),(4,5500)代入y=kx+b求k,b确定表达式,求当x=6时的y值即可;
(2)求销售额w与x之间的函数关系式,利用二次函数的最大值问题求解;
(3)分三种情况讨论假设6月份,7月份,8月份的最大销售为22500万元时,求相应的m值,再分别求出此时另外两月的总利润,通过比较作出判断.
设y=kx+b,根据图象将(2,6500),(4,5500)代入得,
![]() ,
,
解得,![]() ,
,
∴y= -500x+7500,
当x=6时,y= -500×6+7500=4500元;
(2)设销售额为z元,
z=yp=( -500x+7500 )(x+1)= -500x2+7000x+7500= -500(x-7)2+32000,
∵z与x成二次函数,a= -500<0,开口向下,
∴当x=7时,z有最大值,
当x=7时,y=-500×7+7500=4000元.
答:该产品第7个月的销售额最大,该月的销售价格是4000元/台.
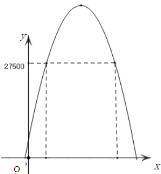
(3)z与x的图象如图的抛物线
当y=27500时,-500(x-7)2+32000=27500,
解得,x1=10,x2=4
∴预计销售部符合销售要求的是4,5,6,7,8,9,10月份.
(4)设总利润为W= -500x2+7000x+7500-m(x+1)= -500x2+(7000-m)x+7500-m,
第一种情况:当x=6时,-500×62+(7000-m) ×6+7500-m=22500,
解得,m=![]() ,
,
此时7月份的总利润为-500×72+(7000-![]() ) ×7+7500-
) ×7+7500-![]() ≈17714<22500,
≈17714<22500,
此时8月份的总利润为-500×82+(7000-![]() ) ×8+7500-
) ×8+7500-![]() ≈19929<22500,
≈19929<22500,
∴当m=![]() 时,6月份利润最大,且最大值为22500万元.
时,6月份利润最大,且最大值为22500万元.
第二种情况:当x=7时,-500×72+(7000-m) ×7+7500-m=22500,
解得,m=1187.5 ,
此时6月份的总利润为-500×62+(7000-1187.5) ×6+7500-1187.5=23187.5>22500,
∴当m=1187.5不符合题意,此种情况不存在.
第三种情况:当x=8时,-500×82+(7000-m) ×8+7500-m=22500,
解得,m=1000 ,
此时7月份的总利润为-500×72+(7000-1000) ×7+7500-1000=24000>22500,
∴当m=1000不符合题意,此种情况不存在.
∴当![]() 时销售利润最大值为22500万元时,此时m=
时销售利润最大值为22500万元时,此时m=![]() .
.