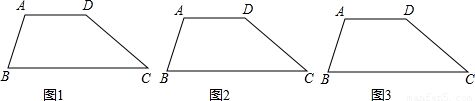
题目内容
某村王大爷家有一块梯形形状的稻田(如图所示),已知:上底AD=40米,下底BC=60米,高h=30米,王大爷准备把这块梯形形状的稻田平均分给两个儿子(面积相等).(1)分割方法有无数种,请你帮助王大爷设计两种不同的分割方案,在图1、图2中分别画出来,并说明理由;
(2)为了尽可能减少筑砌分割田坎的劳动量(只考虑田坎长度对工时的影响,不计其它因素),问:田坎应砌在什么位置最短?请在图3中画出来,并求出此时分割线的长度.
分析:(1)①利用上下底的中点分割,可分割成两个上下底分别相等的梯形;
②连接BD,利用BD的中点O,沿AO和CO分割,即可分割成两个面积相等的四边形ABCO和ADCO;
(2)利用垂线段最短,所以可取①中分割线的中点,过该点作底的垂线段即可,此时该线段等于梯形的高.
②连接BD,利用BD的中点O,沿AO和CO分割,即可分割成两个面积相等的四边形ABCO和ADCO;
(2)利用垂线段最短,所以可取①中分割线的中点,过该点作底的垂线段即可,此时该线段等于梯形的高.
解答:解:(1)方法一:分别取AD、BC的中点E、F,连接EF,线段EF就是所求作的分割线.
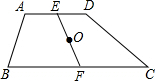 (2分)
(2分)
理由:∵AE=ED,BF=FC,
∴SABEF=
(AE+BF)h=
(ED+FC)h=SEFCD;(3分)
方法二:连接BD,在BD上取中点O,连接AO、CO,折线AOC可以把梯形分割为两个面积相等的图形.
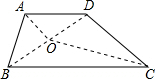
理由:∵BO=OD,∴S△ABO=S△AOD,S△BOC=S△DOC,
∴S'△ABO+S'△BOC=S'△AOD+S'△DOC,
同理,连接AC,取中点O,连接BO、OD,折线BOD可以把梯形分割为两个面积相等的图形;(6分)
方法三:取CD的中点G,过G作FH∥AB,与BC交于F,与AD的延长线交于点H.
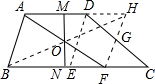
可证:S'△DHG=S'△CFG,则过AF中点O且不穿越△DHG或△CFG或G点的直线均可把梯形面积等分;
(注意:方法(1分),理由(2分),共6分)
(2)田坎应砌在经过EF中点且与AD、BC垂直的线段GH的位置时最短.
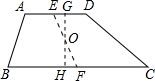
理由:∵O是EF的中点,∴△EOG≌△FOH,
∴S'△EOG=S′△FOH,∴S′ABHG=S′GHDC,
此时,最短线段GH的长度等于高,即为30米.(10分)
 (2分)
(2分)理由:∵AE=ED,BF=FC,
∴SABEF=
| 1 |
| 2 |
| 1 |
| 2 |
方法二:连接BD,在BD上取中点O,连接AO、CO,折线AOC可以把梯形分割为两个面积相等的图形.

理由:∵BO=OD,∴S△ABO=S△AOD,S△BOC=S△DOC,
∴S'△ABO+S'△BOC=S'△AOD+S'△DOC,
同理,连接AC,取中点O,连接BO、OD,折线BOD可以把梯形分割为两个面积相等的图形;(6分)
方法三:取CD的中点G,过G作FH∥AB,与BC交于F,与AD的延长线交于点H.

可证:S'△DHG=S'△CFG,则过AF中点O且不穿越△DHG或△CFG或G点的直线均可把梯形面积等分;
(注意:方法(1分),理由(2分),共6分)
(2)田坎应砌在经过EF中点且与AD、BC垂直的线段GH的位置时最短.

理由:∵O是EF的中点,∴△EOG≌△FOH,
∴S'△EOG=S′△FOH,∴S′ABHG=S′GHDC,
此时,最短线段GH的长度等于高,即为30米.(10分)
点评:本题需仔细分析题意,利用线段的中点即可解决问题.

练习册系列答案
相关题目