Question

【题目】将等腰直角△ABC斜放在平面直角坐标系中，使直角顶点C与点（1，0）重合，点A的坐标为（-2，1）．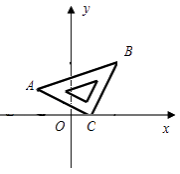

（1）求△ABC的面积S；
（2）求直线AB与y轴的交点坐标．

Answer 1

【答案】
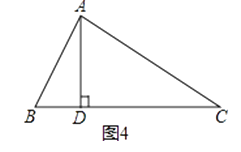
（1）解：过点A作AD⊥x轴，垂足为D．

则AD=1，CD=3， ∴ ，S= =5

（2）解：过点B作BE⊥x轴，垂足为E，

∴∠ADC=∠CEB=90°，则∠CAD+ ∠ACD=90°，

∴∠ACB=90°，则∠BCE+ ∠ACD=90°， ∴∠CAD=∠BCE，

又∵∠ADC=∠CEB=90°，AC=BC，

∴△ADC≌△CEB， ∴CD=BE=3，CE=AD=1，

∴点B的坐标为（2，3）．

设直线AB的解析式为y=kx+b，则 ，

解得： ，

所以y= x+2，

所以直线AB交y轴于点（0，2）

【解析】（1）根据题意和勾股定理求出AD、CD、AC2的值，得到△ABC的面积；（2）根据题意得到△ADC≌△CEB， CD=BE，CE=AD的值，求出点B的坐标，用待定系数法把A、B的坐标代入，求出直线AB的解析式，求出直线AB与y轴的交点坐标．